Властивості кореня n-го степеня. Перетворення виразів, що містять корені
Розглянемо без доведення властивості арифметичних коренів  -го степеня (
-го степеня (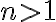 — натуральне число), які узагальнюють відомі властивості квадратного кореня.
— натуральне число), які узагальнюють відомі властивості квадратного кореня.
- 1. Якщо
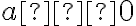 ,
, 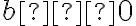 , то
, то ![\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b} \sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}](https://lms.smart-osvita.org/filter/tex/pix.php/8311759534a90a3934464995280f39dd.gif) .
Корінь
.
Корінь  -го степеня з добутку невід’ємних чисел дорівнює добутку коренів із цих чисел.
-го степеня з добутку невід’ємних чисел дорівнює добутку коренів із цих чисел.
Наведена властивість є правильною для будь-якої скінченної кількості невід’ємних чисел.
Наприклад, якщо 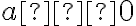 ,
, 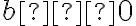 і
і 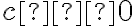 , то
, то ![\sqrt[n]{abc}=\sqrt[n]{(ab)c}=\sqrt[n]{ab}\sqrt[n]{c}=\sqrt[n]{a}\sqrt[n]{b}\sqrt[n]{c}, \sqrt[n]{abc}=\sqrt[n]{(ab)c}=\sqrt[n]{ab}\sqrt[n]{c}=\sqrt[n]{a}\sqrt[n]{b}\sqrt[n]{c},](https://lms.smart-osvita.org/filter/tex/pix.php/756bfcdf8ce5265ff9449dc8e51b9154.gif) тобто
тобто ![\sqrt[n]{abc}=\sqrt[n]{a}\sqrt[n]{b}\sqrt[n]{c} \sqrt[n]{abc}=\sqrt[n]{a}\sqrt[n]{b}\sqrt[n]{c}](https://lms.smart-osvita.org/filter/tex/pix.php/c0dfb73b52ee3b7cba815a2215d5f49c.gif) .
.
Очевидно, що вираз ![\sqrt[n]{ab} \sqrt[n]{ab}](https://lms.smart-osvita.org/filter/tex/pix.php/23fcf815997ac9a6b637fff77ba175bc.gif) при парному
при парному  має зміст, коли
має зміст, коли 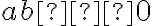 , тобто коли числа
, тобто коли числа  і
і  — одного знака, а значить, і тоді, коли
— одного знака, а значить, і тоді, коли  і
і  — від’ємні. У такому випадку
рівність набуває вигляду
— від’ємні. У такому випадку
рівність набуває вигляду ![\sqrt[n]{ab}=\sqrt[n]{-a}\sqrt[n]{-b} \sqrt[n]{ab}=\sqrt[n]{-a}\sqrt[n]{-b}](https://lms.smart-osvita.org/filter/tex/pix.php/74a211c67d2137b23e7ddc07ad0b7c8b.gif) . Отже,
. Отже, ![\sqrt[n]{ab}=\sqrt[n]{|a|}\sqrt[n]{|b|} \sqrt[n]{ab}=\sqrt[n]{|a|}\sqrt[n]{|b|}](https://lms.smart-osvita.org/filter/tex/pix.php/555641fac958664f5b246ad343092db0.gif) , якщо
, якщо 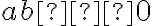 і
і  — парне.
— парне.
Якщо в рівності ![\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b} \sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}](https://lms.smart-osvita.org/filter/tex/pix.php/8311759534a90a3934464995280f39dd.gif) поміняти місцями ліву і праву частини, матимемо тотожність:
поміняти місцями ліву і праву частини, матимемо тотожність: ![\sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{ab} \sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{ab}](https://lms.smart-osvita.org/filter/tex/pix.php/67610febd21c9e73b28dc1efce089f3f.gif) , де
, де 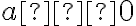 ,
, 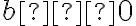 .
Добуток коренів
.
Добуток коренів  -го степеня з невід’ємних чисел дорівнює кореню
-го степеня з невід’ємних чисел дорівнює кореню  -го степеня з добутку цих чисел.
-го степеня з добутку цих чисел.
- 2. Якщо
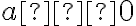 ,
, 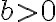 , то
, то ![\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}} \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}](https://lms.smart-osvita.org/filter/tex/pix.php/0c08b8aa8db9fdcd996a5a9b6566ec91.gif) .
Корінь
.
Корінь  -го степеня з дробу, чисельник якого невід’ємний, а знаменник додатний, дорівнює кореню із чисельника, поділеному на корінь із знаменника.
-го степеня з дробу, чисельник якого невід’ємний, а знаменник додатний, дорівнює кореню із чисельника, поділеному на корінь із знаменника.
Очевидно, що корінь із частки при парному  має зміст, коли
має зміст, коли 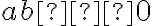 ,
, 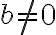 , отже, і тоді, коли
, отже, і тоді, коли 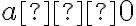 ,
, 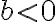 . У цьому випадку
. У цьому випадку ![\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{-a}}{\sqrt[n]{-b}} \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{-a}}{\sqrt[n]{-b}}](https://lms.smart-osvita.org/filter/tex/pix.php/7dce352f5545cc8abe7fdccca4432419.gif) . Отже, якщо
. Отже, якщо 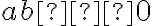 ,
, 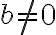 і
і  — парне, то
— парне, то ![\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{|a|}}{\sqrt[n]{|b|}} \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{|a|}}{\sqrt[n]{|b|}}](https://lms.smart-osvita.org/filter/tex/pix.php/98a3738f7aa9bc6f18498287a8a523ea.gif) .
.
Якщо в рівності ![\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}} \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}](https://lms.smart-osvita.org/filter/tex/pix.php/0c08b8aa8db9fdcd996a5a9b6566ec91.gif) поміняти місцями ліву і праву частини, матимемо тотожність:
поміняти місцями ліву і праву частини, матимемо тотожність: ![\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}} \frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}](https://lms.smart-osvita.org/filter/tex/pix.php/9471c9061f5c3f1db4acf929edd55c38.gif) , де
, де 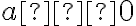 ,
, 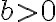 .
Частка, чисельник якої — корінь
.
Частка, чисельник якої — корінь  -го степеня з невід’ємного числа, а знаменник — корінь
-го степеня з невід’ємного числа, а знаменник — корінь  -го степеня з додатного числа, дорівнює кореню
-го степеня з додатного числа, дорівнює кореню  -го степеня із частки цих чисел.
-го степеня із частки цих чисел.
Наприклад, ![\sqrt[4]{\sqrt[7]{2}}=\sqrt[28]{2} \sqrt[4]{\sqrt[7]{2}}=\sqrt[28]{2}](https://lms.smart-osvita.org/filter/tex/pix.php/853a6b31b43b1543bc4a6468a83dddbf.gif) .
.
Якщо  — парне число, то вираз
— парне число, то вираз ![\sqrt[nk]{a^{mk}} \sqrt[nk]{a^{mk}}](https://lms.smart-osvita.org/filter/tex/pix.php/c3c264cf28af22ceecc15e7b1e69f0a3.gif) має зміст при будь-якому дійсному
має зміст при будь-якому дійсному  , і тоді для будь-якого
, і тоді для будь-якого  має місце рівність:
має місце рівність: ![\sqrt[nk]{a^{mk}}=\sqrt[n]{|a|^m} \sqrt[nk]{a^{mk}}=\sqrt[n]{|a|^m}](https://lms.smart-osvita.org/filter/tex/pix.php/83dd6f125f9592895fbc753de373034a.gif) .
.
Домовимося, що корінь першого степеня із числа  дорівнює числу
дорівнює числу  . Це дозволяє використовувати тотожність
. Це дозволяє використовувати тотожність ![\sqrt[nk]{a^{mk}}=\sqrt[n]{a^m} \sqrt[nk]{a^{mk}}=\sqrt[n]{a^m}](https://lms.smart-osvita.org/filter/tex/pix.php/da20105ae2d011e2be0e71a2b5bebe70.gif) і у випадку, коли
і у випадку, коли 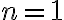 .
.
Наприклад, ![\sqrt[8]{3^6}=\sqrt[4]{3^3} \sqrt[8]{3^6}=\sqrt[4]{3^3}](https://lms.smart-osvita.org/filter/tex/pix.php/d289d65cd86ee4509311b2d02f2a0a22.gif) .
.
Властивість  іноді називають основною властивістю арифметичного кореня.
іноді називають основною властивістю арифметичного кореня.
Наприклад, ![(\sqrt[6]{8})^2=\sqrt[6]{8^2}=\sqrt[6]{64}=2 (\sqrt[6]{8})^2=\sqrt[6]{8^2}=\sqrt[6]{64}=2](https://lms.smart-osvita.org/filter/tex/pix.php/beb585da0c19ac1f97dfe990c700724f.gif) .
.
Наприклад, порівняємо числа ![\sqrt[5]{4} \sqrt[5]{4}](https://lms.smart-osvita.org/filter/tex/pix.php/8af9e819e3e31e95be24b16f8acf3131.gif) і
і ![\sqrt[3]{3} \sqrt[3]{3}](https://lms.smart-osvita.org/filter/tex/pix.php/00183145853114fdd8d947a663084fb6.gif) .
Зведемо корені до одного показника, користуючись основною властивістю арифметичного кореня:
.
Зведемо корені до одного показника, користуючись основною властивістю арифметичного кореня: ![\sqrt[5]{4}=\sqrt[15]{64} \sqrt[5]{4}=\sqrt[15]{64}](https://lms.smart-osvita.org/filter/tex/pix.php/8b5ecd862e3e697f02953a07cf6a766a.gif) ,
, ![\sqrt[3]{3}=\sqrt[15]{243} \sqrt[3]{3}=\sqrt[15]{243}](https://lms.smart-osvita.org/filter/tex/pix.php/3ccfb2eca07f5a509785991c09dba921.gif) , тобто
, тобто ![\sqrt[5]{4}\lt\sqrt[3]{3} \sqrt[5]{4}\lt\sqrt[3]{3}](https://lms.smart-osvita.org/filter/tex/pix.php/927d08d878ba08fa117baf9f601de971.gif) .
.
Властивість 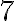 надає можливість порівнювати арифметичні корені.
надає можливість порівнювати арифметичні корені.
Властивості арифметичного кореня  -го степеня використовують для тотожних перетворень виразів: винесення множника з-під знака кореня, внесення множника під знак кореня, звільнення від ірраціональності у знаменнику дробу, спрощення ірраціональних виразів.
-го степеня використовують для тотожних перетворень виразів: винесення множника з-під знака кореня, внесення множника під знак кореня, звільнення від ірраціональності у знаменнику дробу, спрощення ірраціональних виразів.
Задача. Винеси множник з-під знака кореня: ![\sqrt[4]{324} \sqrt[4]{324}](https://lms.smart-osvita.org/filter/tex/pix.php/39d01043cbf48e9da10d2633671f5b6f.gif) .
.
Розв’язання. Виконуючи цю дію, підкореневий вираз слід подати у вигляді добутку множників, з яких (одного або кількох) можна добути корінь. ![\sqrt[4]{324}=\sqrt[4]{81 \cdot 4}=\sqrt[4]{3^4 \cdot 2^2}=3\sqrt{2} \sqrt[4]{324}=\sqrt[4]{81 \cdot 4}=\sqrt[4]{3^4 \cdot 2^2}=3\sqrt{2}](https://lms.smart-osvita.org/filter/tex/pix.php/4719bb78a863e3e7bd64fccfc339ebad.gif) .
.
- 2. Внесення множника під знак кореня. Розглядаючи перетворення винесення множника з-під знака кореня у зворотному порядку, отримаємо перетворення, яке називають внесенням множника під знак кореня.
Задача. Внеси множник під знак кореня: ![-2 \cdot \sqrt[4]{8} -2 \cdot \sqrt[4]{8}](https://lms.smart-osvita.org/filter/tex/pix.php/ba976c3335e479979a7c2a7f67524502.gif) .
.
Розв’язання. Вносячи множник під знак кореня, треба піднести його до степеня, який дорівнює показнику кореня, і записати як множник під знаком кореня.
![-2 \cdot \sqrt[4]{8}=-1 \cdot 2 \sqrt[4]{8}=-\sqrt[4]{2^4 \cdot 8}=-\sqrt[4]{16 \cdot 8}=-\sqrt[4]{128} -2 \cdot \sqrt[4]{8}=-1 \cdot 2 \sqrt[4]{8}=-\sqrt[4]{2^4 \cdot 8}=-\sqrt[4]{16 \cdot 8}=-\sqrt[4]{128}](https://lms.smart-osvita.org/filter/tex/pix.php/f167bb2b9f54ef6779c1aef6f8670431.gif) .
.
- 3. Звільнення від ірраціональності у знаменнику дробу. Нагадаємо, що звільнитися від ірраціональності у знаменнику (чисельнику) дробу означає виконати такі перетворення цього дробу, щоб його знаменник (чисельник) не містив знака кореня.
Задача. Звільнитися від ірраціональності в знаменнику дробу 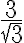 .
.
Розв’язання. Звільняючись від ірраціональності в знаменнику дробу, необхідно чисельник і знаменник дробу помножити або поділити на одне
й те саме число або вираз, відмінний від нуля.
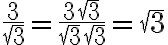 .
.
Джерела:
1. О.С. Істер, О.В. Єргіна. Алгебра і початки аналізу: підручник для 10-го класу. 2018 рік. Шкільні підручники онлайн. URL: https://pidruchnyk.com.ua/1223-algebra-10-klas-ister.html
2. М.І. Бурда,Т.В. Колесник,Ю.І. Мальований, Н.А. Тарасенкова. Математика (алгебра і початки аналізу та геометрія): підручник для 10-го класу. 2018 рік. Шкільні підручники онлайн. URL: https://pidruchnyk.com.ua/402-matematika-burda-kolesnik-malovaniy-tarasenkova-10-klas.html
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour
![\sqrt[3]{8 \cdot 27}=\sqrt[3]{8} \cdot \sqrt[3]{27}=2\cdot 3=6 \sqrt[3]{8 \cdot 27}=\sqrt[3]{8} \cdot \sqrt[3]{27}=2\cdot 3=6](https://lms.smart-osvita.org/filter/tex/pix.php/45bb245740c6218966f258980d3006a0.gif)
![\sqrt[5]{4} \cdot \sqrt[5]{8} = \sqrt[5]{4 \cdot 8} = \sqrt[5]{32} = 2 \sqrt[5]{4} \cdot \sqrt[5]{8} = \sqrt[5]{4 \cdot 8} = \sqrt[5]{32} = 2](https://lms.smart-osvita.org/filter/tex/pix.php/ff0620d88059dd3c877f35b7ae7ce06b.gif)
![\sqrt[3]{\frac{8}{27}}=\frac{\sqrt[3]{8}}{\sqrt[3]{27}}=\frac{2}{3} \sqrt[3]{\frac{8}{27}}=\frac{\sqrt[3]{8}}{\sqrt[3]{27}}=\frac{2}{3}](https://lms.smart-osvita.org/filter/tex/pix.php/a2979cb68857ebab8dea268100335be3.gif)
![\frac{\sqrt[5]{486}}{\sqrt[5]{2}}=\sqrt[5]{\frac{486}{2}}=\sqrt[5]{243}=3 \frac{\sqrt[5]{486}}{\sqrt[5]{2}}=\sqrt[5]{\frac{486}{2}}=\sqrt[5]{243}=3](https://lms.smart-osvita.org/filter/tex/pix.php/fcb79f024e942f161c990175345e4274.gif)
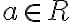
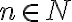
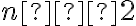
![\sqrt[n]{a^n}=\begin{cases}|a|, & \text{якщо}\, n \, -\, \text{парне}, \\ a, & \text{якщо}\, n \, -\, \text{непарне}. \end{cases} \sqrt[n]{a^n}=\begin{cases}|a|, & \text{якщо}\, n \, -\, \text{парне}, \\ a, & \text{якщо}\, n \, -\, \text{непарне}. \end{cases}](https://lms.smart-osvita.org/filter/tex/pix.php/2cd91e3c2a892baca42fa4bc7de69480.gif)
![\sqrt[5]{7^5}=7 \sqrt[5]{7^5}=7](https://lms.smart-osvita.org/filter/tex/pix.php/116b955fdac593f9fd47eca76895ded4.gif)
![\sqrt[4]{(-2)^4} =|-2|=2 \sqrt[4]{(-2)^4} =|-2|=2](https://lms.smart-osvita.org/filter/tex/pix.php/fd5140c96ca1b9fcf4713bdd4397d27a.gif)
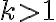
![\sqrt[n]{\sqrt[k]{a}}=\sqrt[nk]{a} \sqrt[n]{\sqrt[k]{a}}=\sqrt[nk]{a}](https://lms.smart-osvita.org/filter/tex/pix.php/18e63066010edd6772b4a99395d4ae93.gif)
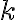
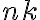
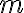
![(\sqrt[n]{a})^k=\sqrt[n]{a^k} (\sqrt[n]{a})^k=\sqrt[n]{a^k}](https://lms.smart-osvita.org/filter/tex/pix.php/9109cd76ffde2f231fbb883dcc497935.gif)
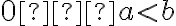
![\sqrt[n]{a}< \sqrt[n]{b} \sqrt[n]{a}< \sqrt[n]{b}](https://lms.smart-osvita.org/filter/tex/pix.php/b3ba0dea2eb976d59f0346b0fa0ef5a5.gif)