Розв’язки рівняння x^n=a
З означення кореня 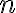 -го степеня випливає, що добути корінь
-го степеня випливає, що добути корінь  -го степеня з дійсного числа
-го степеня з дійсного числа  — це все одно, що знайти дійсні розв’язки рівняння:
— це все одно, що знайти дійсні розв’язки рівняння: 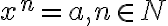 .
.
Розв’яжемо його графічно.
Нехай у рівнянні 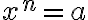 маємо випадок, коли
маємо випадок, коли  — парне.
— парне.
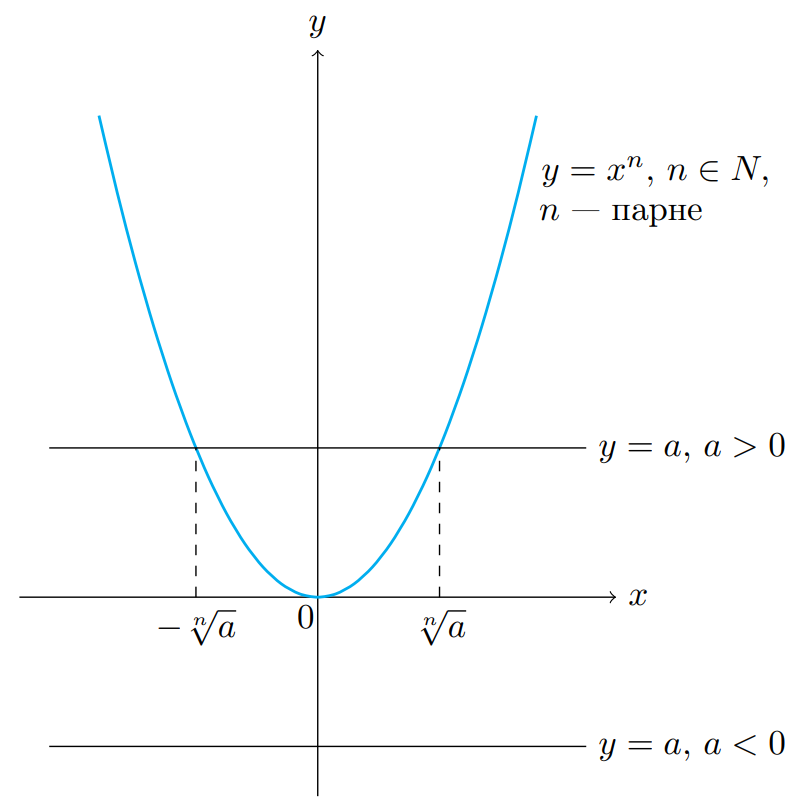
Побудуємо графіки функцій 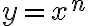 ,
,  — парне, і
— парне, і 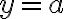 .
.
Бачимо, що якщо 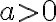 , то графіки перетинатимуться у двох точках, тобто рівняння
, то графіки перетинатимуться у двох точках, тобто рівняння 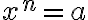 матиме два корені.
матиме два корені.
Оскільки ![(\sqrt[n]{a})^n=a (\sqrt[n]{a})^n=a](https://lms.smart-osvita.org/filter/tex/pix.php/c9591708d0e4a2e5951619f26c40bc2e.gif) і
і ![(-\sqrt[n]{a})^n=a (-\sqrt[n]{a})^n=a](https://lms.smart-osvita.org/filter/tex/pix.php/60f3df1c1905ef12f48c822a2de880b0.gif) , то
, то ![x_1=\sqrt[n]{a} x_1=\sqrt[n]{a}](https://lms.smart-osvita.org/filter/tex/pix.php/03995a0546f4f3e4197ce37d7a6e18f7.gif) і
і ![x_2 = -\sqrt[n]{a} x_2 = -\sqrt[n]{a}](https://lms.smart-osvita.org/filter/tex/pix.php/fa692999dd46090360ffd33957b27b8b.gif) — корені рівняння
— корені рівняння 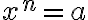 у випадку парного
у випадку парного  .
.
Якщо 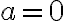 , то рівняння
, то рівняння 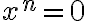 має єдиний корінь — число
має єдиний корінь — число 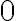 .
.
Якщо 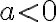 , при парному
, при парному  рівняння
рівняння 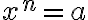 коренів не має.
коренів не має.
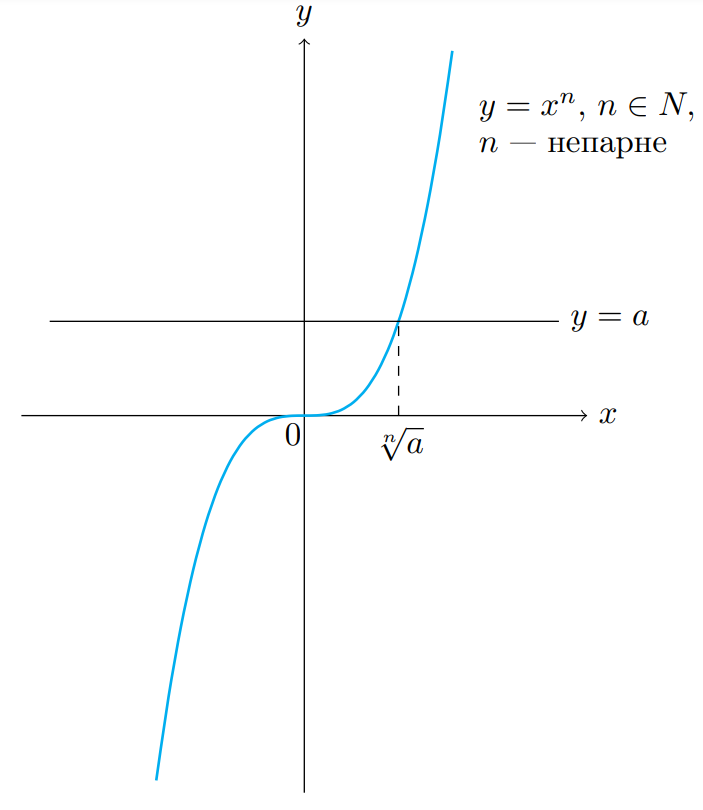
Нехай  — непарне. Тоді для будь-якого
— непарне. Тоді для будь-якого  рівняння
рівняння 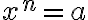 має єдиний корінь.
має єдиний корінь.
Оскільки ![(\sqrt[n]{a})^n=a (\sqrt[n]{a})^n=a](https://lms.smart-osvita.org/filter/tex/pix.php/c9591708d0e4a2e5951619f26c40bc2e.gif) , то
, то ![x=\sqrt[n]{a} x=\sqrt[n]{a}](https://lms.smart-osvita.org/filter/tex/pix.php/a48edfe4aa725b7661d32ee62d4a0743.gif) — єдиний корінь рівняння
— єдиний корінь рівняння 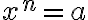 , коли
, коли  — непарне.
— непарне.
Систематизуємо дані про розв’язки рівняння 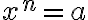 у вигляді схеми.
у вигляді схеми.

Джерело: О.С. Істер, О.В. Єргіна. Алгебра і початки аналізу: підручник для 10-го класу. 2018 рік. Шкільні підручники онлайн. URL: https://pidruchnyk.com.ua/1223-algebra-10-klas-ister.html
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour