Корінь n-го степеня. Арифметичний корінь n-го степеня
Нагадаємо, що квадратним коренем із числа  називають таке число, квадрат якого дорівнює
називають таке число, квадрат якого дорівнює  .
.
Наприклад, числа 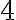 і
і 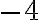 — квадратні корені із числа
— квадратні корені із числа 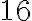 , бо
, бо 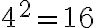 і
і 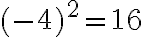 ;
; 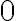 — квадратний корінь із числа
— квадратний корінь із числа 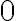 , оскільки
, оскільки 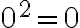 ; квадратного кореня із числа
; квадратного кореня із числа 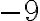 не існує, бо немає числа, квадрат якого дорівнює
не існує, бо немає числа, квадрат якого дорівнює 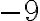 .
.
Квадратний корінь називають ще коренем другого степеня.
Подібно до коренів другого степеня існують також корені третього, четвертого, …,  -го степеня.
-го степеня.
Коренем  -го степеня з числа
-го степеня з числа  називають число,
називають число,  -й степінь якого дорівнює
-й степінь якого дорівнює  .
.
Наприклад, корінь третього степеня із числа 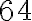 дорівнює
дорівнює 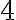 , оскільки
, оскільки 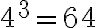 . Числа
. Числа 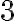 і
і 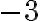 є коренями четвертого степеня із числа
є коренями четвертого степеня із числа 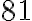 , бо
, бо 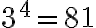 і
і 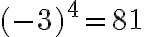 . Коренем п’ятого степеня із числа
. Коренем п’ятого степеня із числа 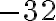 є число
є число 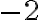 , оскільки
, оскільки 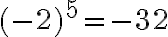 .
.
Як і для квадратного кореня, для кореня  -го степеня розглянемо поняття арифметичного кореня. Нагадаємо, що арифметичним квадратним коренем із числа
-го степеня розглянемо поняття арифметичного кореня. Нагадаємо, що арифметичним квадратним коренем із числа  називають таке невід’ємне число, квадрат якого дорівнює
називають таке невід’ємне число, квадрат якого дорівнює  .
.
Невід’ємний корінь  -го степеня з невід’ємного числа
-го степеня з невід’ємного числа  називають арифметичним коренем
називають арифметичним коренем  -го степеня з числа
-го степеня з числа  .
.
При 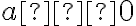 для арифметичного значення кореня
для арифметичного значення кореня  -го степеня з числа
-го степеня з числа  існує спеціальне позначення:
існує спеціальне позначення: ![\sqrt[n]{a} \sqrt[n]{a}](https://lms.smart-osvita.org/filter/tex/pix.php/bf7ff33f3b129b15c06203d60f007807.gif) , де
, де  — підкореневий вираз,
— підкореневий вираз, ![\sqrt[ ]{ } \sqrt[ ]{ }](https://lms.smart-osvita.org/filter/tex/pix.php/4634167a20aec29bc62a264c1879fdaa.gif) — знак кореня,
— знак кореня,  — показник кореня. Залежно від показників корені бувають другого, третього і вищих степенів. Показник кореня — завжди число натуральне.
— показник кореня. Залежно від показників корені бувають другого, третього і вищих степенів. Показник кореня — завжди число натуральне.
Наприклад, те, що корінь третього степеня з числа 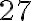 дорівнює
дорівнює 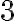 (оскільки
(оскільки 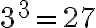 і
і 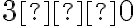 ), записують так:
), записують так: ![\sqrt[3]{27}=3 \sqrt[3]{27}=3](https://lms.smart-osvita.org/filter/tex/pix.php/25ee31010c9e17e82b9b35f0ca6ef6dc.gif) ; те, що корінь четвертого степеня із
; те, що корінь четвертого степеня із 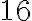 дорівнює
дорівнює  (оскільки
(оскільки 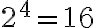 і
і 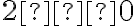 ), записують так:
), записують так: ![\sqrt[4]{16}=2 \sqrt[4]{16}=2](https://lms.smart-osvita.org/filter/tex/pix.php/874e47eb3e4068a9fd8869b748113f58.gif) . Але для запису того, що корінь четвертого степеня із
. Але для запису того, що корінь четвертого степеня із 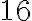 дорівнює
дорівнює 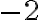 , позначення немає.
, позначення немає.
При 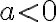 значення кореня
значення кореня  -го степеня з числа а існує тільки при непарних значеннях
-го степеня з числа а існує тільки при непарних значеннях  (оскільки не існує такого дійсного числа, парний степінь якого буде від’ємним числом). У цьому випадку корінь непарного степеня
(оскільки не існує такого дійсного числа, парний степінь якого буде від’ємним числом). У цьому випадку корінь непарного степеня  із числа
із числа  теж позначають
теж позначають ![\sqrt[n]{a} \sqrt[n]{a}](https://lms.smart-osvita.org/filter/tex/pix.php/bf7ff33f3b129b15c06203d60f007807.gif) . Наприклад, те, що корінь третього степеня з числа
. Наприклад, те, що корінь третього степеня з числа 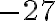 дорівнює
дорівнює 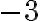 (бо
(бо 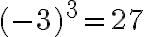 ), записують так:
), записують так: ![\sqrt[3]{-27} =-3 \sqrt[3]{-27} =-3](https://lms.smart-osvita.org/filter/tex/pix.php/10cd51a3ea92ab7343a25add9e5bcecb.gif) . Оскільки
. Оскільки 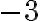 — від’ємне число, то
— від’ємне число, то ![\sqrt[3]{-27} \sqrt[3]{-27}](https://lms.smart-osvita.org/filter/tex/pix.php/b4175615e338ac1c0262407f1476de73.gif) не є арифметичним значенням кореня. Але корінь непарного степеня з від’ємного числа можна виразити через арифметичне значення кореня за допомогою формули
не є арифметичним значенням кореня. Але корінь непарного степеня з від’ємного числа можна виразити через арифметичне значення кореня за допомогою формули ![\sqrt[2k+1]{-a}=- \sqrt[2k+1]{a} \sqrt[2k+1]{-a}=- \sqrt[2k+1]{a}](https://lms.smart-osvita.org/filter/tex/pix.php/6135ecc50e531188e7abeae18d89163a.gif) .
.
Зазначимо також, що значення ![\sqrt[2k+1]{a} \sqrt[2k+1]{a}](https://lms.smart-osvita.org/filter/tex/pix.php/d67d5928d0bc5231fd23d05fd76d077c.gif) має той самий знак, що й число
має той самий знак, що й число  , оскільки при піднесенні до непарного степеня знак числа не змінюється.
, оскільки при піднесенні до непарного степеня знак числа не змінюється.
Отже,
- якщо
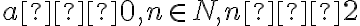 , то вираз
, то вираз ![\sqrt[n]{a} \sqrt[n]{a}](https://lms.smart-osvita.org/filter/tex/pix.php/bf7ff33f3b129b15c06203d60f007807.gif) означає арифметичний корінь
означає арифметичний корінь  -го степеня із числа
-го степеня із числа  ;
; - якщо
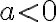 , то при непарному
, то при непарному  вираз
вираз ![\sqrt[n]{a} \sqrt[n]{a}](https://lms.smart-osvita.org/filter/tex/pix.php/bf7ff33f3b129b15c06203d60f007807.gif) означає корінь
означає корінь  -го степеня із числа
-го степеня із числа  , а при парному
, а при парному  цей вираз не має змісту.
цей вираз не має змісту.
Доходимо висновку, що вираз ![\sqrt[n]{a} \sqrt[n]{a}](https://lms.smart-osvita.org/filter/tex/pix.php/bf7ff33f3b129b15c06203d60f007807.gif) при парному
при парному  має зміст лише для
має зміст лише для 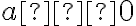 , при непарному
, при непарному  — для будь-якого значення
— для будь-якого значення  .
.
Також за означенням кореня n-го степеня можна записати, що в тому випадку, коли існує значення ![\sqrt[n]{a} \sqrt[n]{a}](https://lms.smart-osvita.org/filter/tex/pix.php/bf7ff33f3b129b15c06203d60f007807.gif) , виконується рівність
, виконується рівність ![(\sqrt[n]{a})^n=a (\sqrt[n]{a})^n=a](https://lms.smart-osvita.org/filter/tex/pix.php/c9591708d0e4a2e5951619f26c40bc2e.gif) .
.
Обчислення значень коренів n-го степеня з чисел називають добуванням коренів із цих чисел.
Джерела:
1. Г.П. Бевз, В.Г. Бевз, Н.Г. Владімірова. Алгебра і початки аналізу: підручник для 10-го класу. 2018 рік. Шкільні підручники онлайн. URL: https://pidruchnyk.com.ua/1169-algebr-bevz-10-klas.html
2. Є.П. Нелін. Алгебра і початки аналізу: підручник для 10-го класу. 2018 рік. Шкільні підручники онлайн. URL: https://pidruchnyk.com.ua/427-algebra-neln-10-klas.html
3. О.С. Істер, О.В. Єргіна. Алгебра і початки аналізу: підручник для 10-го класу. 2018 рік. Шкільні підручники онлайн. URL: https://pidruchnyk.com.ua/1223-algebra-10-klas-ister.html
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour