Розв’язуємо повне квадратне рівняння за допомогою теореми Вієта
Ще раз пригадаємо, що квадратне рівняння, старший коефіцієнт якого дорівнює 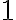 , називається зведеним. Зведене квадратне рівняння можна розв’язувати за допомогою наслідка з теореми Вієта. Якщо
, називається зведеним. Зведене квадратне рівняння можна розв’язувати за допомогою наслідка з теореми Вієта. Якщо 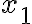 і
і 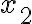 — корені зведеного квадратного рівняння
— корені зведеного квадратного рівняння 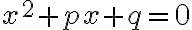 , то
, то 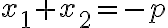 ,
,  . Іншими словами, сума коренів зведеного квадратного рівняння дорівнює другому коефіцієнту, узятому з протилежним знаком, а добуток коренів дорівнює вільному члену.
. Іншими словами, сума коренів зведеного квадратного рівняння дорівнює другому коефіцієнту, узятому з протилежним знаком, а добуток коренів дорівнює вільному члену.
Також, розглянемо наслідок з теореми, оберненої до теореми Вієта. Якщо числа 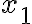 і
і 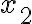 такі, що
такі, що 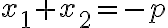 ,
,  , то ці числа є коренями зведеного квадратного рівняння
, то ці числа є коренями зведеного квадратного рівняння 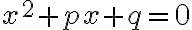 . Цей наслідок дає змогу розв’язувати деякі квадратні рівняння усно, не використовуючи формулу коренів квадратного рівняння.
. Цей наслідок дає змогу розв’язувати деякі квадратні рівняння усно, не використовуючи формулу коренів квадратного рівняння.

ПРИКЛАД 2

ПРИКЛАД 3

ПРИКЛАД 4
За допомогою теореми Вієта можна скласти квадратне рівняння, якщо відомі його корені.

Джерело:
А.Г. Мерзляк, В.Б. Полонський, М.С. Якір. Алгебра: підручник для 8-го класу з поглибленим вивченням математики. 2021 рік. Шкільні підручники онлайн. URL: https://files.pidruchnyk.com.ua/uploads/book/8-klas-alhebra-merzlyak-2021-pohlyb.pdf
Приклади із "Мій клас"
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour