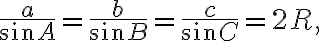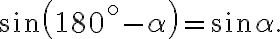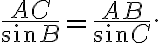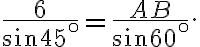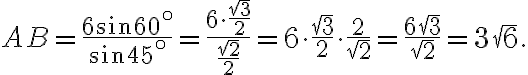Математика jul_2024_9_5: Теорема синусів | Smartosvita LMS

Теорема синусів

Теорема синусів є однією з найкрасивіших теорем у тригонометрії, яка застосовується до будь-якого трикутника і встановлює зв’язок між довжинами сторін трикутника та синусами його кутів.

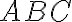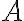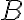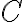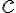Нехай у довільному трикутнику $ABC$ навпроти кутів $A$ , $B$ , $C$ лежать сторони $a$ , $b$ та $c$ відповідно.

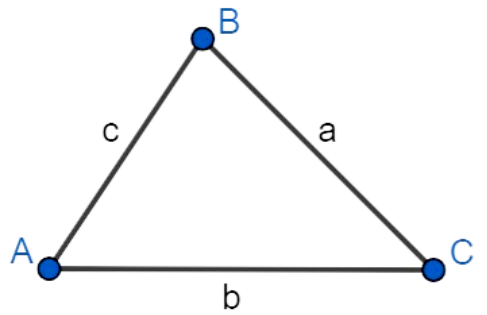
Тоді за теоремою синусів маємо:

$\frac{a}{ \sin A} = \frac{b}{ \sin B} = \frac{c}{ \sin C} = 2R,$

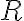де $R$ — радіус кола, описаного навколо трикутника $ABC$ .

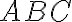У випадку, коли один з кутів є тупим, скористаємося формулою:

$\sin \left(180^{\circ}-\alpha\right)=\sin \alpha.$

Задача. Знайди сторону 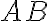$AB$ у трикутнику 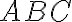$ABC$ , якщо відомо, що 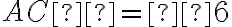$AC = 6$ см, $\angle B = 45^\circ$ , $\angle C = 60^\circ.$

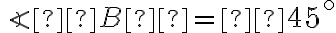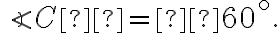
Розв’язання. За теоремою синусів маємо:

$\frac{AC}{ \sin B} = \frac{AB}{ \sin C}.$

Підставивши числові значення з умови, отримаємо:

$\frac{6}{ \sin 45^\circ } = \frac{AB}{ \sin 60^\circ}.$

Звідки маємо:

$AB=\frac{6 \sin 60^\circ }{ \sin 45^\circ }=\frac{6 \cdot \frac{\sqrt3}{2}}{ \frac{\sqrt2}{2}}=6 \cdot \frac{\sqrt3}{2} \cdot \frac{2}{\sqrt2}= \frac{6\sqrt3}{\sqrt2}=3\sqrt6.$

Відповідь: 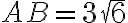$AB = 3 \sqrt6$ см.

Теорію розробила Грибель Ольга з використанням ChatGPT-3.5.

Метод оцінювання: Краща оцінка.