Ланкова робота. Розв’язування систем графічним способом (2)
Умови завершення
Розглянемо всі три випадки.
Система лінійних рівнянь
Система лінійних рівнянь
Система лінійних рівнянь \begin{cases} a_1x+b_1y=c_1,\\a_2x+b_2y=c_2, \end{cases} має нескінченну кількість розв’язків, коли прямі збігаються, а коефіцієнти при всіх змінних будуть пропорційними:
Текст розробила Дубей Наталія з використанням матеріалів з платформи Khan Academy.
Система лінійних рівнянь зазвичай має єдиний розв’язок (прямі перетинаються), але іноді вона може не мати жодного розв’язку (паралельні прямі) або мати нескінченну кількість розв’язків (одна пряма).
Розглянемо всі три випадки.
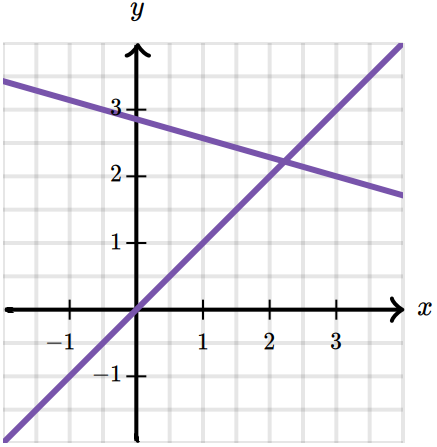
Один розв’язок.
Система лінійних рівнянь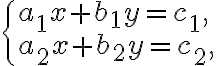 
має один розв’язок, якщо прямі, які є графіками рівнянь, будуть перетинатися в одній точці, а коефіцієнти при змінних не будуть пропорційними: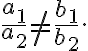 
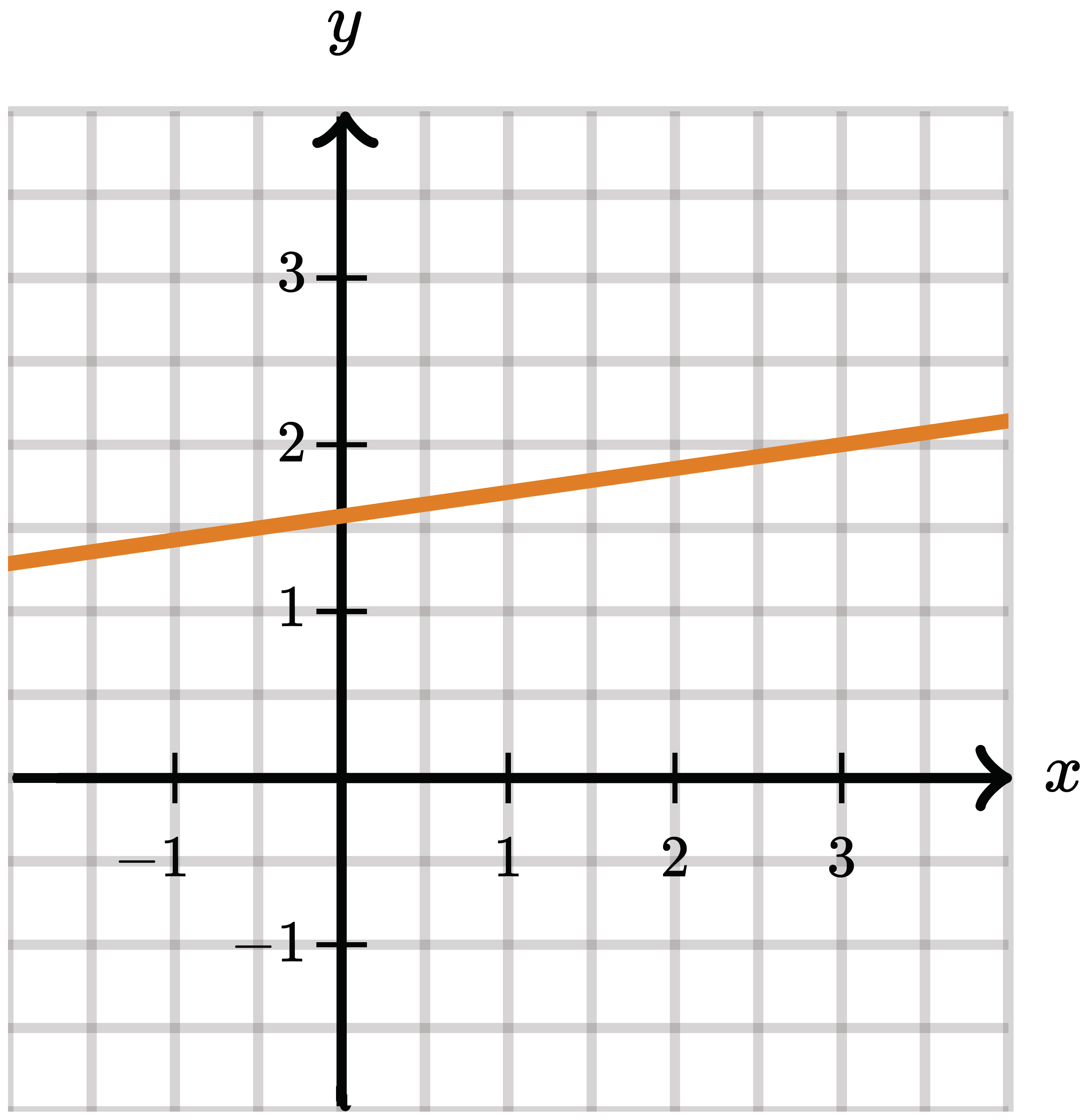
Не має розв’язку.
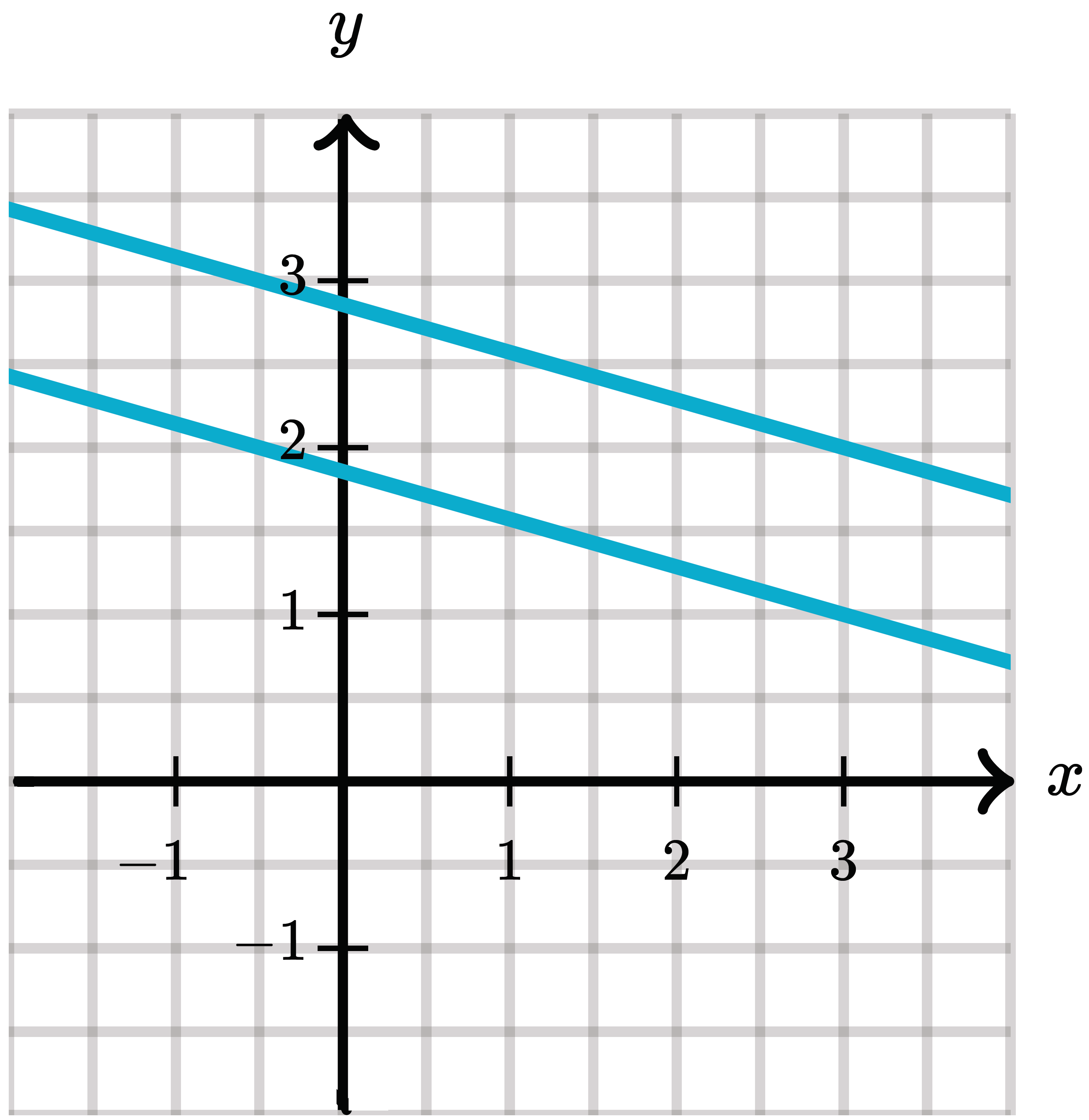
Система лінійних рівнянь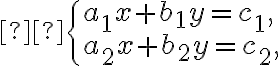
не має розв’язку, якщо прямі будуть паралельні, а коефіцієнти при змінних будуть пропорційними, проте не пропорційні вільним членам: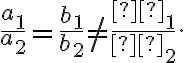 
Безліч розв’язків.
Система лінійних рівнянь \begin{cases} a_1x+b_1y=c_1,\\a_2x+b_2y=c_2, \end{cases} має нескінченну кількість розв’язків, коли прямі збігаються, а коефіцієнти при всіх змінних будуть пропорційними: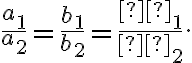 
Текст розробила Дубей Наталія з використанням матеріалів з платформи Khan Academy.
Метод оцінювання: Краща оцінка.