Математика jun_2024_6_12: НСД та НСК | Smartosvita LMS

НСД та НСК

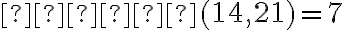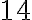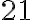Найбільшим спільним дільником (НСД) кількох чисел називають найбільше число, на яке ділиться кожне із заданих чисел. Наприклад, $НСД (14, 21) = 7$ , бо і $14$ , і $21$ діляться одночасно на 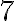$7$ , і при цьому це найбільше число, на яке вони одночасно діляться. Розглянемо алгоритм знаходження НСД двох чисел на конкретному прикладi.

Приклад: обчислити найбільший спільний дільник чисел $156$ і $852$ .

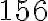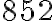Розкладемо числа $156$ і $852$ на прості множники та підкреслимо їхні спільні дільники.

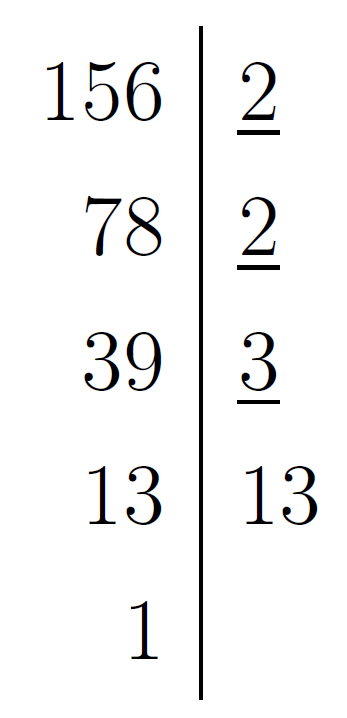
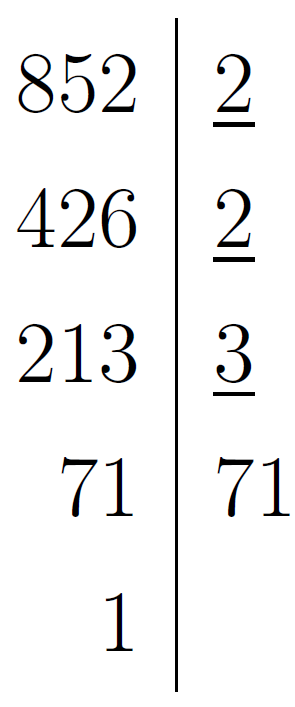
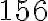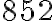Тоді найбільший спільний дільник чисел $156$ та $852$ дорівнює добутку підкреслених чисел (спільних простих дільникiв), тобто $НСД (156,852) = 2\cdot2\cdot3 = 12$ .

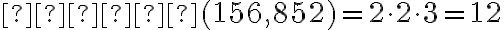НСД взаємно простих чисел дорівнює одиниці, оскільки вони не мають спільних дільників.

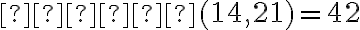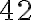Найменшим спільним кратним (НСК) кількох чисел називають найменше число, яке ділиться на кожне із заданих чисел. Наприклад, $НСК (14,21) = 42$ , бо $42$ ділиться і на 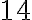$14$ , і на 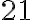$21$ , і при цьому є найменшим.

Приклад: обчислити найменше спільне кратне чисел $156$ і $852$ .

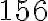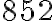Розкладемо числа $156$ і $852$ на прості множники та підкреслимо їхні спільні дільники.

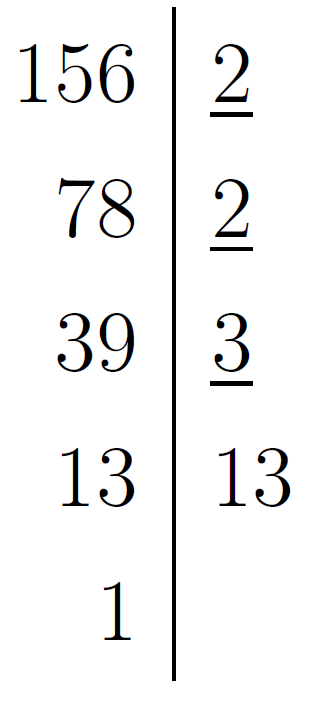
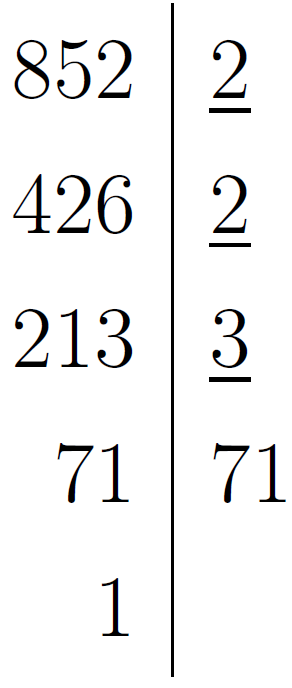
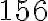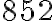Тоді найменше спільне кратне чисел $156$ та $852$ дорівнює добутку першого числа на непідкреслені цифри другого числа, або навпаки, тобто

$НСК(156, 852) = 156 \cdot 71 = 11076$

або

$НСК(156,852) = 852\cdot13 = 11076$ .

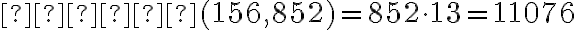НСК взаємно простих чисел дорівнює їх добутку, оскільки вони не мають спільних дільникiв, а отже, в другому числі жодна з цифр не буде підкреслена. Тому ми множитимемо перше число на кожну з цифр розкладу другого числа, добуток яких і дорівнює другому числу.

Розглянемо на прикладi: обчислити найменше спільне кратне чисел 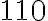$110$ і $273$ .

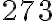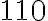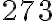Розкладемо числа $110$ і $273$ на прості множники та підкреслимо їхні спільні дільники, якщо вони будуть.

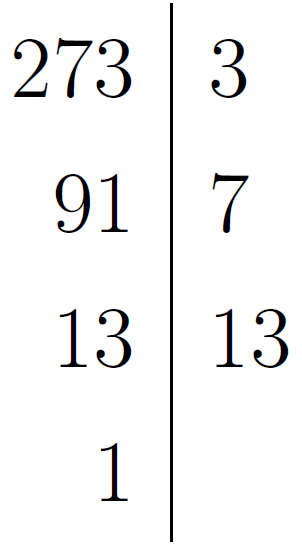
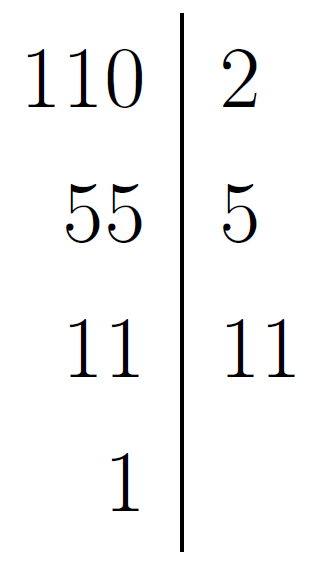
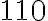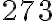Тоді найменше спільне кратне чисел $110$ та $273$ дорівнює добутку першого числа на непідкреслені цифри другого числа, тобто $НСК(110,273) = 110\cdot3\cdot7\cdot13= 110\cdot273 = 30030$ .

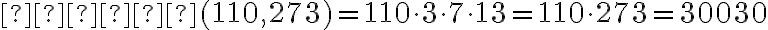_{Теорію розробив Чоп'юк Юрій}

Метод оцінювання: Краща оцінка.

Accessibility

Background Colour

Font Face

Font Kerning

Font Size

1

Image Visibility

Letter Spacing

0

Line Height

1.2

Link Highlight

Text Colour