Прості та складені числа
Прості числа — це особливі числа, які можна поділити тільки на самих себе і на 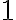 . Якщо спробувати поділити їх на будь-яке інше число, то вийде залишок. Наприклад, число
. Якщо спробувати поділити їх на будь-яке інше число, то вийде залишок. Наприклад, число  можна поділити тільки на
можна поділити тільки на  і на
і на 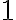 . Це і робить його простим числом.
. Це і робить його простим числом.
Але якщо взяти число 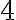 , то його можна поділити не тільки на
, то його можна поділити не тільки на 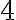 і
і 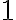 , але і на
, але і на  . Тому
. Тому 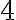 не є простим числом. Такі числа називають складеними.
не є простим числом. Такі числа називають складеними.
Приклади простих чисел:  ,
, 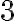 ,
,  ,
, 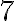 ,
, 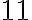 ,
, 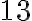
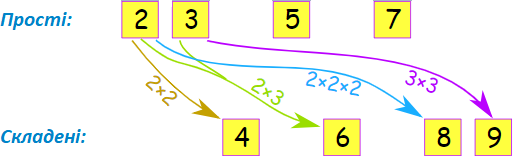
Чому важливі прості числа? Вони як будівельні блоки для інших чисел. Уяви, що кожне складене число — це конструктор, який можна скласти з простих чисел. Наприклад, число 6 можна отримати, помноживши прості числа 2 і 3.
Прості числа використовуються у комп’ютерах для захисту інформації.
Основні факти про прості числа:
- Простих чисел існує безліч, і вони продовжуються без кінця.
- Найменше просте число — це 2, яке також є єдиним парним простим числом.
- Коли розглядаємо великі числа, то там важче знайти прості числа, але вони завжди там є!
Як ми можемо визначити, чи є число простим?
Простий спосіб (ну майже) — спробувати поділити число на всі числа до нього (крім 1 і самого себе) і подивитися, чи є якесь число, на яке воно ділиться без залишку. Якщо немає, то це просте число!
Теорію розробили Чоп'юк Юрій та Дубей Наталія з використанням ChatGPT-4.0.
Картинку взято з https://www.mathsisfun.com/prime-factorization.html/
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour