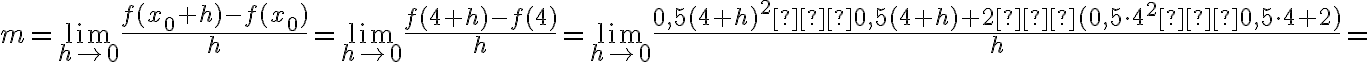Математика jul_2024_10_3: Нахил дотичної та миттєва швидкість зміни | Smartosvita LMS

Нахил дотичної та миттєва швидкість зміни

Швидкість зміни — це відношення зміни однієї змінної до зміни іншої змінної. Типовим прикладом цього є швидкість. Швидкість — це відношення зміни відстані до зміни часу. Швидкість зміни може бути або середньою, або миттєвою. Але що таке миттєва швидкість зміни? Миттєва швидкість зміни — це показник того, наскільки швидко змінюється зв’язок між двома змінними в будь-якій точці. Відношення між двома змінними можна описати за допомогою функції. Миттєву швидкість зміни часто називають похідною, оскільки її можна знайти шляхом диференціації функції двох змінних.
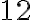Щоб зрозуміти різницю між середньою швидкістю зміни та миттєвою швидкістю зміни, розглянемо приклад із автомобілем, який проїжджає $5$ кілометрів. Дорога автомобілем займає $12$ хвилин. Це означає, що середня швидкість становила 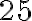$25$ км/год. Однак у якийсь момент під час поїздки спідометр на автомобілі показав 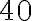$40$ кілометів за годину. Це була миттєва швидкість автомобіля в той момент часу.

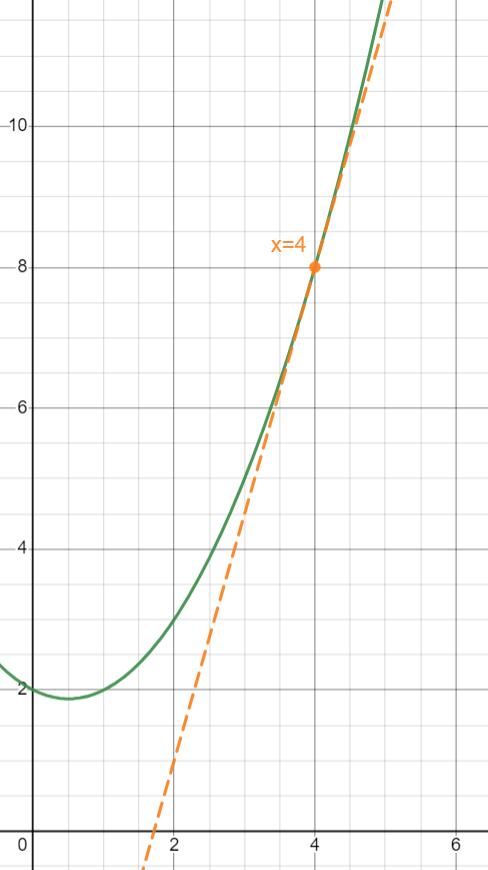
На графіку миттєва швидкість зміни представлена як дотична до основної функції в одній точці. Щоб знайти цю швидкiсть змiни, потрiбно обчислити нахил дотичної в цій точцi. Чому так? Дуже важливо було зрозуміти, що середня швидкість зміни між двома точками — це те саме, що нахил січної. І коли ці точки стають все ближче і ближче одна до одної, і оскільки січна з’єднує ці дві точки разом, ця відстань між точками, між значеннями $x$ точок, наближається до $0$ . 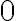Відповідно при наближенні точок одна до одної нахили січних будуть все ближче до нахилу дотичної лінії в певній точці.

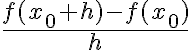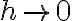Оскільки нахил січної обчислюється за формулою $\frac{f(x_0+h)-f(x_0)}{h}$ , а $h \rightarrow 0$ , то нахил дотичної ми можемо обчислити за формулою:

$m= \lim \limits_{ h \rightarrow 0}\frac{f(x_0+h)-f(x_0)}{h}$ , (*)

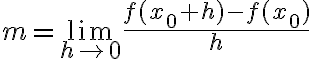якщо границя існує.

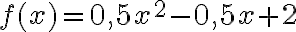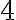Приклад. Інтернет-підприємець заснував компанiю i визначив таку функцiю для розрахунку доходу компанiї (в мiльйонах доларiв США): $f(x)=0,5x^2-0,5x+2$ , де $x$ — це кiлькiсть тижнiв. Знайди миттєву швидкiсть змiни через $4$ тижнi.
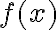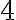Розв’язання. Нам потрібно знайти миттєву швидкість зміни функції $f(x)$ через $4$ тижні. Тобто у цьому випадку на графіку функції ми мали б провести дотичну у точці $x=4$ .

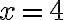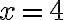Обчислимо нахил цієї дотичної за формулою (*), підставивши значення $x=4$ . Отримаємо:

$m= \lim \limits_{ h \rightarrow 0}\frac{f(x_0+h)-f(x_0)}{h}= \lim \limits_{ h \rightarrow 0}\frac{f(4+h)-f(4)}{h}=\lim \limits_{ h \rightarrow 0} \frac{0,5(4+h)^2−0,5(4+h)+2−(0,5 \cdot4^2 −0,5 \cdot 4+2)}{h}=$

$=\lim \limits_{ h \rightarrow 0} \frac{4h+0,5h^2-0,5h}{h}=\lim \limits_{ h \rightarrow 0}(4+0,5h-0,5)=4-0,5=3,5$ .

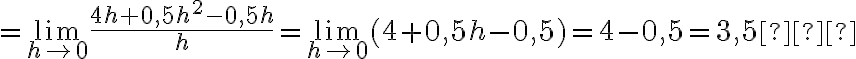Множимо це значення на 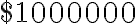$$1000000$ , щоб отримати правильну вiдповiдь, оскiльки дохiд розраховується в мiльйонах доларiв: $3,5 \cdot $1000000 =$3500000$ .
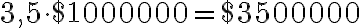Миттєва швидкiсть змiни доходу компанiї через чотири тижнi дорiвнює 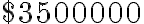$$3500000$ на тиждень.

Джерело:

Khan Academy
Study.com
House of Math

Метод оцінювання: Краща оцінка.