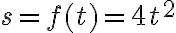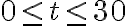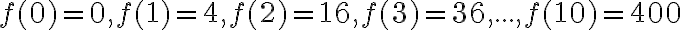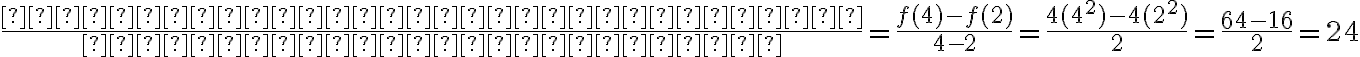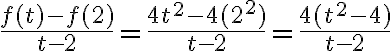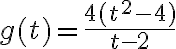Границя
Історично розвиток числення Ісааком Ньютоном (1642–1727) і Готфрідом Вільгельмом Лейбніцом (1646–1716) став результатом дослідження таких проблем:
1) знаходження дотичної до кривої в заданій точці кривої (рис. 1а);
2) знаходження площі плоскої області, обмеженої довільною кривою (рис. 1б).
Рисунок 1а. Чому дорівнює нахил дотичної 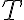 у точці
у точці 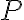 ?
?
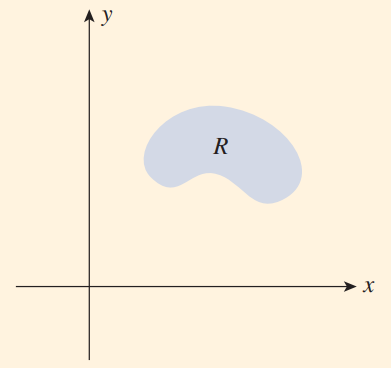
Рисунок 1б. Чому дорівнює площа області  ?
?
Проблема дотичної може здатися не пов’язаною з будь-яким практичним застосуванням математики, але, як ти побачиш пізніше, проблема знаходження швидкості зміни однієї величини відносно іншої математично еквівалентна геометричній задачі знаходження нахилу дотичної до кривої в даній точці кривої. Саме відкриття зв’язку між цими двома проблемами було поштовхом до розвитку числення в XVII столітті та зробило його таким незамінним інструментом для вирішення практичних завдань. Нижче наведено кілька прикладів таких проблем:
- знаходження швидкості руху об’єкта;
- знаходження швидкості зміни популяції бактерій відносно часу;
- знаходження швидкості зміни прибутку компанії відносно часу;
- знаходження швидкості зміни доходу туристичного агентства відносно витрат агентства на рекламу.
Дослідження проблеми дотичної призвело до створення диференціального числення, яке базується на понятті похідної функції. Дослідження проблеми площі призвело до створення інтегрального числення, яке базується на понятті антипохідної або інтеграла функції. Похідна функції та інтеграл функції тісно пов’язані. Як похідна функції, так і інтеграл функції визначаються за допомогою більш фундаментального поняття — границя.
Із даних, отриманих під час випробування, проведеного на прототипі маглева (потяга на магнітній підвісці), який рухається по прямій монорейковій колії, інженери визначили, що положення маглева (у сантиметрах) від початку координат у момент часу  (в секундах) задано:
(в секундах) задано:
де
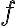 називається функцією положення маглева. Положення маглева в момент часу
називається функцією положення маглева. Положення маглева в момент часу 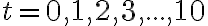 , виміряне від початкового положення, становить
, виміряне від початкового положення, становитьсантиметрів (рис. 2).
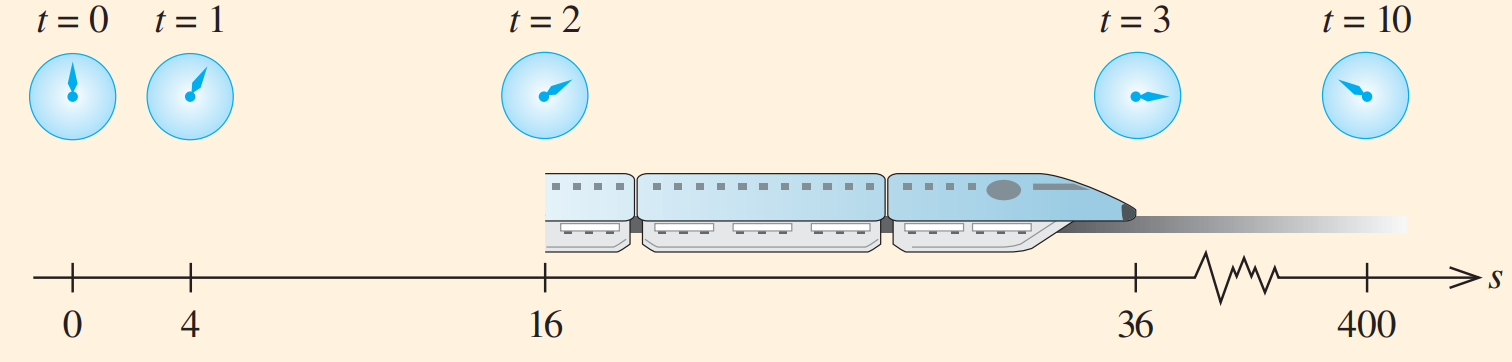
Рисунок 2
Припустимо, ми хочемо знайти швидкість маглева в момент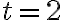 . Це значення швидкості маглева, яке відображене на його спідометрі у цей конкретний момент часу. Обчислення цієї величини за допомогою лише рівняння (1) видається неможливим завданням; але подумайте, які величини ми можемо обчислити за допомогою цього співвідношення. Очевидно, що ми можемо обчислити положення маглева у будь-який момент
. Це значення швидкості маглева, яке відображене на його спідометрі у цей конкретний момент часу. Обчислення цієї величини за допомогою лише рівняння (1) видається неможливим завданням; але подумайте, які величини ми можемо обчислити за допомогою цього співвідношення. Очевидно, що ми можемо обчислити положення маглева у будь-який момент 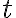 , як ми робили раніше для деяких вибраних значень
, як ми робили раніше для деяких вибраних значень 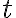 . Використовуючи ці значення, ми можемо обчислити середню швидкість маглева за певний проміжок часу. Наприклад, середня швидкість потяга на проміжку часу
. Використовуючи ці значення, ми можемо обчислити середню швидкість маглева за певний проміжок часу. Наприклад, середня швидкість потяга на проміжку часу ![[2;~ 4] [2;~ 4]](https://lms.smart-osvita.org/filter/tex/pix.php/41a283dc8f59b15d07259e9989a02366.gif) визначається так:
визначається так: або
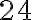 см/год.
см/год.Хоча це не зовсім швидкість маглева в момент часу
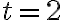 , це дає нам наближення до його швидкості у цей час.
, це дає нам наближення до його швидкості у цей час.Чи можемо ми виконати це завдання краще? Інтуїтивно зрозуміло, що чим менший інтервал часу ми виберемо (з
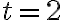 як лівої кінцевої точки), тим більше середня швидкість за цей проміжок часу наближатиметься до фактичної швидкості маглева при
як лівої кінцевої точки), тим більше середня швидкість за цей проміжок часу наближатиметься до фактичної швидкості маглева при 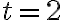 .
.Тепер опишемо цей процес загальними термінами. Нехай
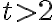 . Тоді середня швидкість маглева за проміжок часу
. Тоді середня швидкість маглева за проміжок часу ![[2;~ t] [2;~ t]](https://lms.smart-osvita.org/filter/tex/pix.php/4f319b6f26f54aeeff8f4ea211869642.gif) обчислюється за формулою:
обчислюється за формулою: Вибираючи значення
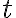 все ближче і ближче до
все ближче і ближче до  , ми отримуємо послідовність чисел, які дають середні швидкості маглева за все менші й менші проміжки часу. Як ми вже помітили раніше, ця послідовність чисел повинна наближатися до миттєвої швидкості потяга в
, ми отримуємо послідовність чисел, які дають середні швидкості маглева за все менші й менші проміжки часу. Як ми вже помітили раніше, ця послідовність чисел повинна наближатися до миттєвої швидкості потяга в 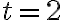 .
.Спробуємо виконати деякі прикладні обчислення. Використовуючи рівняння (2) і вибираючи послідовність значень t
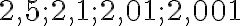 та
та 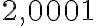 , яка наближається до
, яка наближається до  , ми отримаємо:
, ми отримаємо:середня швидкість за проміжок часу
![[2;~ 2,5] [2;~ 2,5]](https://lms.smart-osvita.org/filter/tex/pix.php/ed0b185ae5f4693886743b7e807083a5.gif) становить
становить 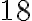 сантиметрів за секунду;
сантиметрів за секунду;середня швидкість за проміжок часу
![[2; 2,1] [2; 2,1]](https://lms.smart-osvita.org/filter/tex/pix.php/1743ca5c305562cb7c26aded8ccc6a59.gif) становить
становить 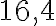 сантиметрів за секунду
сантиметрів за секундуі так далі.
Ці результати узагальнені в таблиці 1.
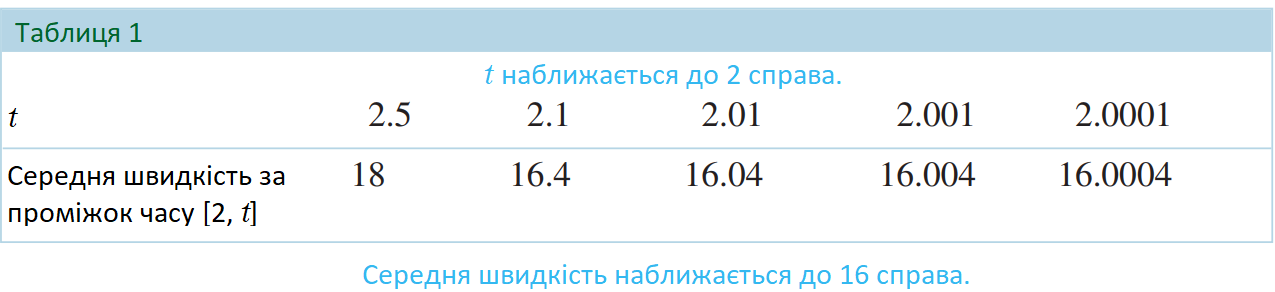
З таблиці 1 ми бачимо, що середня швидкість маглева, здається, наближається до числа 16, оскільки вона обчислюється за все менші проміжки часу. Ці обчислення показують, що миттєва швидкість потяга в момент 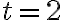 становить
становить 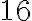 сантиметрів за секунду.
сантиметрів за секунду.
Примітка. Зауваж, що ми не можемо отримати миттєву швидкість для маглева при 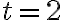 , підставляючи
, підставляючи 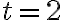 у рівняння (2), оскільки це значення
у рівняння (2), оскільки це значення 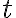 не належить області визначення функції середньої швидкості.
не належить області визначення функції середньої швидкості.
Розглянемо функцію 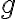 , визначену так:
, визначену так:
яка зображує середню швидкість маглева (див. рівняння (2)). Припустимо, ми повинні визначити значення, до якого 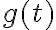 наближається, коли
наближається, коли 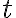 наближається до (фіксованого) числа
наближається до (фіксованого) числа  . Якщо ми візьмемо послідовність значень
. Якщо ми візьмемо послідовність значень 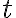 , що наближаються до
, що наближаються до  , з правого боку, як ми робили раніше, ми бачимо, що
, з правого боку, як ми робили раніше, ми бачимо, що 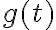 наближається до числа
наближається до числа 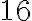 . Подібним чином, якщо ми візьмемо послідовність значень
. Подібним чином, якщо ми візьмемо послідовність значень 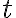 , що наближаються до
, що наближаються до  зліва, наприклад
зліва, наприклад 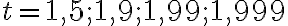 і
і 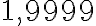 , ми отримаємо результати, наведені в таблиці 2.
, ми отримаємо результати, наведені в таблиці 2.
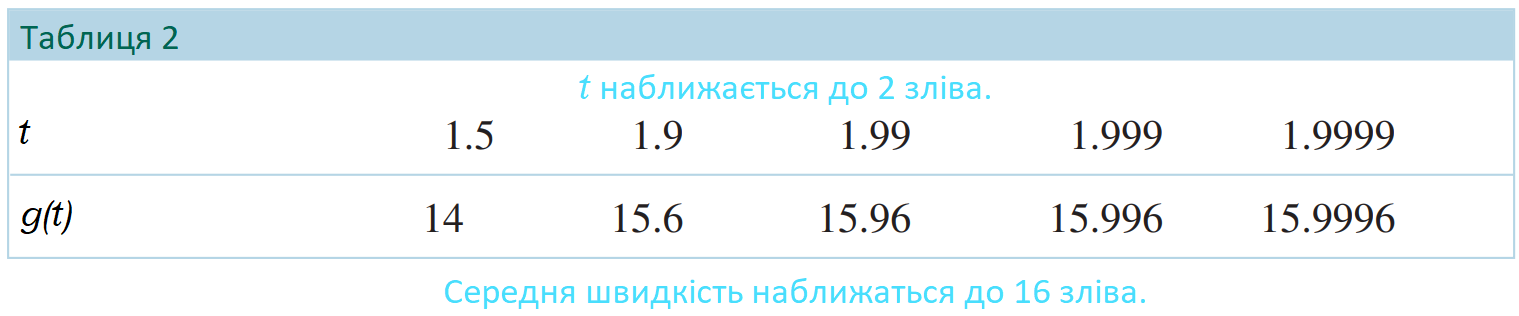
Зверни увагу, що  наближається до числа
наближається до числа  , коли
, коли  наближається до
наближається до  — цього разу з лівого боку. Іншими словами, коли
— цього разу з лівого боку. Іншими словами, коли 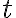 наближається до
наближається до  з обох сторін від
з обох сторін від  ,
, 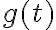 наближається до
наближається до 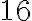 . У цій ситуації ми говоримо, що границя
. У цій ситуації ми говоримо, що границя 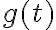 , коли
, коли 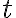 прямує до
прямує до  , дорівнює
, дорівнює 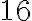 , записується
, записується 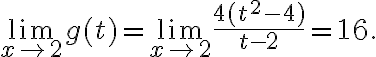
Графік функції 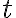 , зображений на рисунку 3, підтверджує це спостереження.
, зображений на рисунку 3, підтверджує це спостереження.
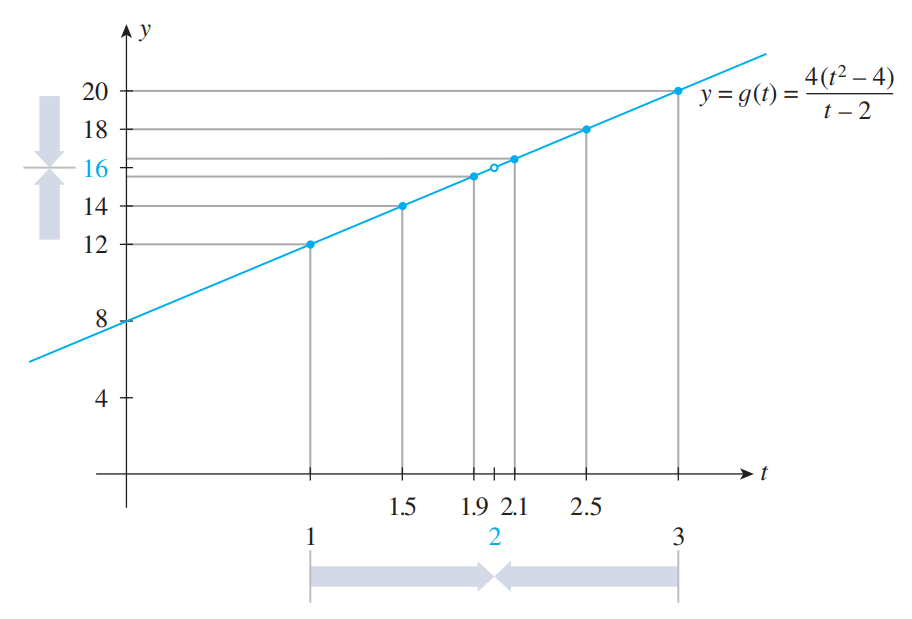
Рисунок 3
Зверни увагу, що точка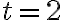 не належить області визначення функції
не належить області визначення функції 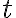 (з цієї причини точка
(з цієї причини точка 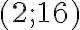 відсутня на графіку
відсутня на графіку 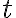 ). Проте це не важливо, оскільки значення
). Проте це не важливо, оскільки значення 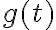 при
при 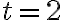 , якщо таке є, не впливає на обчислення границі.
, якщо таке є, не впливає на обчислення границі.Цей приклад приводить до наступного неформального означення.
Функція
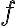 має границю
має границю 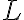 , коли
, коли  прямує до
прямує до  , записується як
, записується як 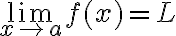 , якщо значення
, якщо значення 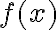 можна зробити як завгодно близьким до числа
можна зробити як завгодно близьким до числа 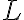 , взявши
, взявши  достатньо близьким до (але не рівним)
достатньо близьким до (але не рівним)  .
.
Розглянемо приклад обчислення границі. Нехай
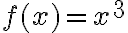 — і обчислимо
— і обчислимо 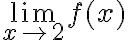 .
.Розв’язання. Графік функції
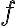 показаний на рис. 4.
показаний на рис. 4.
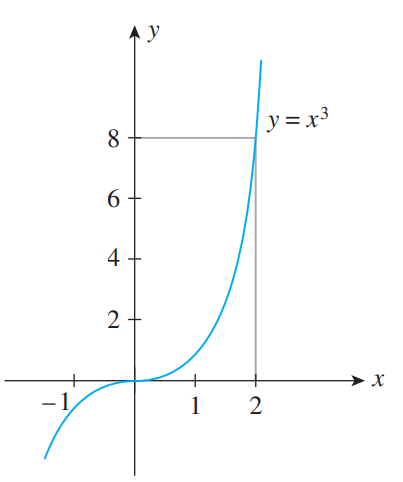
Рисунок 4
Ти можеш побачити, що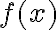 можна наблизити до числа
можна наблизити до числа 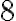 як завгодно, взявши
як завгодно, взявши  достатньо близьким до
достатньо близьким до  . Таким чином,
. Таким чином, 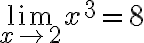 .
.
Джерело: Applied Mathematics: For the Managerial, Life, and Social Sciences (5th Edition). Tan S.T.
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour