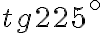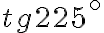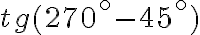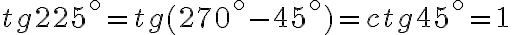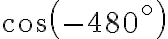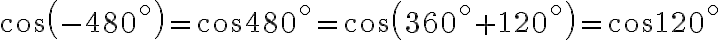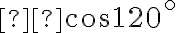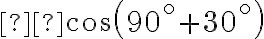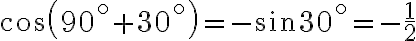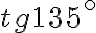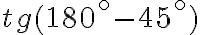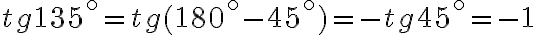Формули зведення
Формули зведення — це формули перетворення тригонометричних функцій кута, за допомогою яких тригонометричні функції від аргументів виду 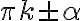 і
і 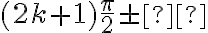 , де
, де 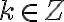 , зводяться до тригонометричних функцій від аргументу
, зводяться до тригонометричних функцій від аргументу 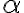 .
.
Всі формули зведення подано в таблиці:
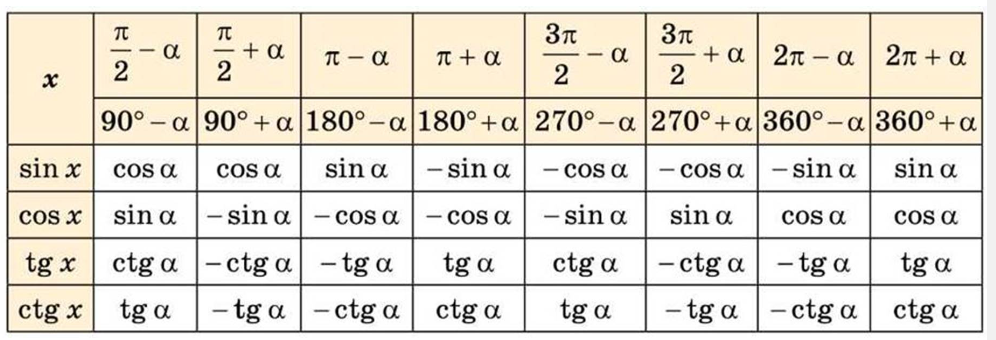
Однак запам’ятати всі ці формули досить важко та й не потрібно. Простіше їх вивести.
При вертикальному діаметрі 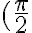 або
або 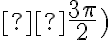 функція міняється на протилежну і має той знак, що початкова функція у даній чверті; при горизонтальному діаметрі
функція міняється на протилежну і має той знак, що початкова функція у даній чверті; при горизонтальному діаметрі 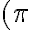 або
або 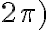 — залишається тією ж.
— залишається тією ж.
Приклад 1.
Розв’язання.
Оскільки в дужках маємо 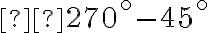 , то функцію змінюємо на протилежну (
, то функцію змінюємо на протилежну ( 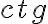 ). Тепер глянемо знак початкової функції (
). Тепер глянемо знак початкової функції ( 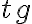 ) в даній чверті.
) в даній чверті.
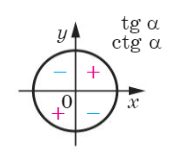
Кут 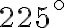 належить третій чверті. Бачимо з рисунка, що тангенс у цій чверті додатний. Отже, маємо:
належить третій чверті. Бачимо з рисунка, що тангенс у цій чверті додатний. Отже, маємо:
Приклад 2.
Розв’язання.
Спочатку віднімемо період косинуса, а саме 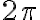 , тобто
, тобто 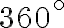 :
:
Оскільки маємо 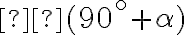 , то функцію змінюємо на протилежну.
, то функцію змінюємо на протилежну.
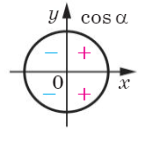
Косинус в даній чверті від’ємний, отже, маємо:
Приклад 3.
Розв’язання.
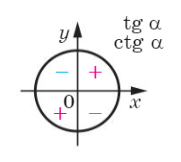
Оскільки маємо горизонтальний діаметр ( 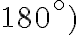 , то функцію залишаємо без змін. Тангенс у даній чверті від’ємний.
, то функцію залишаємо без змін. Тангенс у даній чверті від’ємний.
Джерела:
1. О. Істер. Математика: підручник для 10-го класу. 2018 рік. Шкільні підручники онлайн. URL: https://pidruchnyk.com.ua/430-algebra-proflniy-rven-merzlyak-10-klas.html
2. Алгебра і початки аналізу: проф. рівень : підруч. для 10 кл. закладів загальної середньої освіти / А. Г. Мерзляк, Д. А. Номіровський, В. Б. Полонський, М. С. Якір. — Х. : Гімназія, 2018. — 400 с. : іл. ISBN 978-966-474-311-9. URL:https://pidruchnyk.com.ua/430-algebra-proflniy-rven-merzlyak-10-klas.html
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour