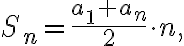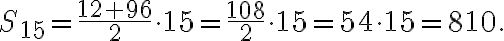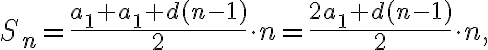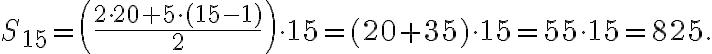Сума n перших членів арифметичної прогресії
Пригадаємо, що арифметична прогресія — це послідовність чисел, де різниця між будь-якими двома послідовними членами є сталою. Наприклад, послідовність 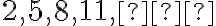 є арифметичною прогресією, де кожен наступний член більший за попередній на
є арифметичною прогресією, де кожен наступний член більший за попередній на 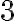 .
.
Дуже часто в задачах на арифметичну прогресію потрібно знайти суму декількох перших членів прогресії. Для цього використовують формулу суми  перших членів арифметичної прогресії:
перших членів арифметичної прогресії:
де
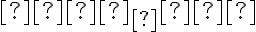 — сума перших
— сума перших 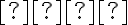 членів прогресії;
членів прогресії;
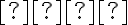 — кількість перших членів, суму яких потрібно знайти;
— кількість перших членів, суму яких потрібно знайти;
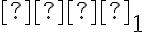 — перший член прогресії;
— перший член прогресії;
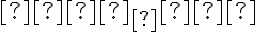 —
—  -й член прогресії.
-й член прогресії.
Задача:
 На шкільних канікулах Марійка вирішила читати книги. У перший день вона прочитала
На шкільних канікулах Марійка вирішила читати книги. У перший день вона прочитала 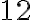 сторінок, а кожного наступного дня збільшувала кількість прочитаних сторінок на одне і те саме число. Скільки всього сторінок вона прочитає за
сторінок, а кожного наступного дня збільшувала кількість прочитаних сторінок на одне і те саме число. Скільки всього сторінок вона прочитає за 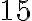 днів, якщо вона планує прочитати
днів, якщо вона планує прочитати 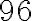 сторінок на п’ятнадцятий день?
сторінок на п’ятнадцятий день?
Розв’язання. За умовою задачі: 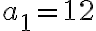 сторінок,
сторінок, 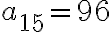 сторінок,
сторінок, 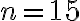 днів. Підставивши дані значення у формулу
днів. Підставивши дані значення у формулу 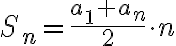 , отримуємо:
, отримуємо:
Отже, за 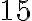 днів Марійка прочитає
днів Марійка прочитає 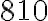 сторінок.
сторінок.
Якщо пригадати, що 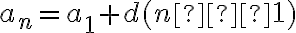 і підставити праву частину даної рівності в попередню формулу, то отримуємо другу формулу для обчислення cуми
і підставити праву частину даної рівності в попередню формулу, то отримуємо другу формулу для обчислення cуми  перших членів арифметичної прогресії:
перших членів арифметичної прогресії:
де 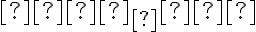 — сума перших
— сума перших 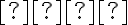 членів прогресії;
членів прогресії;
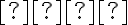 — кількість перших членів, суму яких потрібно знайти;
— кількість перших членів, суму яких потрібно знайти;
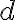 — різниця арифметичної прогресії.
— різниця арифметичної прогресії.
Цю формулою зручно використовувати у випадку, коли задано перший член та різницю прогресії.
Задача:
 Надихнувшись прикладом Марійки, Миколка теж вирішив присвятити час читанню книг під час шкільних канікул. У перший день він прочитав
Надихнувшись прикладом Марійки, Миколка теж вирішив присвятити час читанню книг під час шкільних канікул. У перший день він прочитав 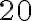 сторінок, а кожного наступного дня він читав на
сторінок, а кожного наступного дня він читав на  сторінок більше, ніж у попередній. Скільки всього сторінок він прочитає за
сторінок більше, ніж у попередній. Скільки всього сторінок він прочитає за 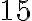 днів?
днів?
Розв’язання. За умовою задачі: 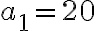 сторінок,
сторінок, 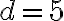 сторінок,
сторінок, 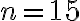 днів. Підставивши дані значення у формулу
днів. Підставивши дані значення у формулу 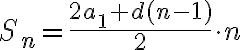 , отримуємо:
, отримуємо:
Отже, за 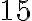 днів Миколка прочитає
днів Миколка прочитає 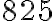 сторінок.
сторінок.
Теорію розробила Грибель Ольга з використанням ChatGPT-3.5.
Картинку до прикладів згенерував
Чоп'юк Юрій в ChatGPT 4o.
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour