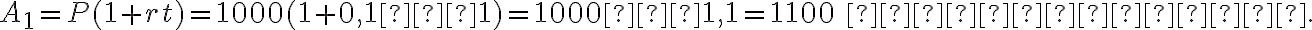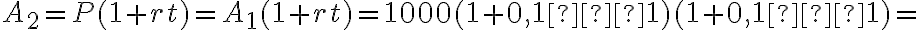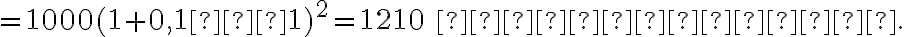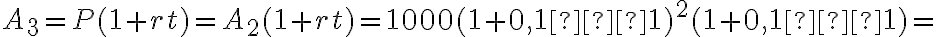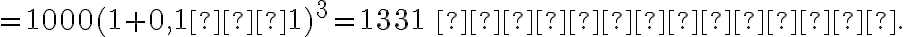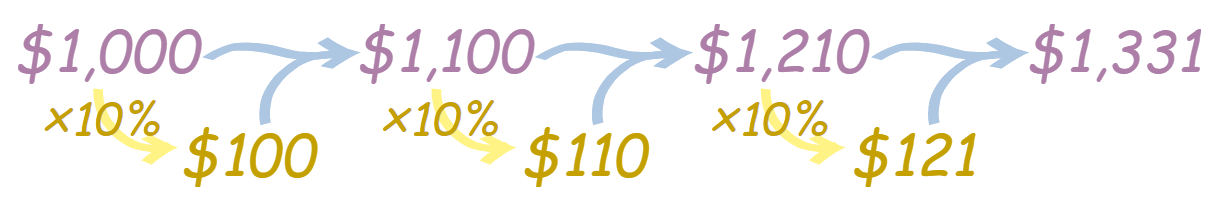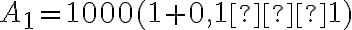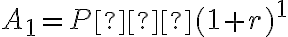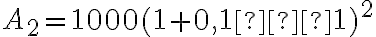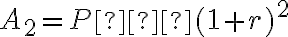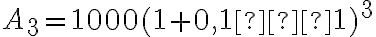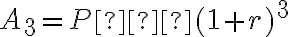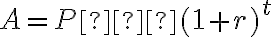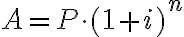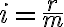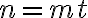Математика jul_2024_9_5: Складний відсоток | Smartosvita LMS

Складний відсоток

Уяви, що ти вирішив розмістити кошти на банківському рахунку або інвестувати їх в інвестиційний фонд, що пропонує певний річний відсоток прибутку. Але чи знаєш ти, що банки та інвестиційні фонди зазвичай використовують складні відсотки, а не прості? Тому давай детальніше розглянемо, що таке складний відсоток та чим він відрізняється від простого відсотка.

На відміну від простого відсотка, при складному відсотку нарахування (нараховані відсотки) додаються до початкової суми вкладу, і в наступному році відсотки нараховуються вже на цю збільшену суму. Таким чином, щороку ти заробляєш відсотки не лише на вкладених грошах, але й на вже нарахованих відсотках.

Пригадаймо приклад з Алексом, щоб краще зрозуміти як працює складний відсоток. Нехай Алекс поклав 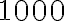$1000$ доларів на свій банківський рахунок під 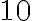$10$ складних відсотків.

Перший рік: Алекс починає з 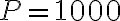$P=1000$ доларів. Протягом першого року він заробляє 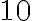$10$ % на свою початкову суму, і тепер загальна сума на його рахунку становить

$A_1=P(1+rt)=1000(1+0,1⋅1)=1000⋅1,1=1100 \text{ доларів.}$

Другий рік: Алекс продовжує заробляти відсотки на 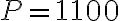$P=1100$ доларів (тепер це його нова початкова сума), і на кінець другого року загальна сума на його рахунку становить

$A_2=P(1+rt)=A_1(1+rt)=1000(1+0,1⋅1)(1+0,1⋅1)=$

$=1000(1+0,1⋅1)^2=1210 \text{ доларів.}$

Третій рік: тепер Алекс заробляє відсотки на свою нову початкову суму 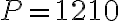$P=1210$ доларів, і на кінець третього року загальна сума на його рахунку становить

$A_3=P(1+rt)=A_2(1+rt)=1000(1+0,1⋅1)^2(1+0,1⋅1)=$

$=1000(1+0,1⋅1)^3=1331 \text{ доларів.}$

Цей процес буде продовжуватись і надалі. Щороку Алекс буде заробляти відсотки на зростаючу суму грошей, що дозволить йому збільшувати свої заощадження значно швидше, ніж у разі простого відсотка.

Звісно, мова може йти не тільки про інвестиції, але також про кредити. Коли ти береш у банку кредит, та сама ідея складних відсотків застосовується в зворотному напрямку. Ти позичаєш певну суму грошей (початковий капітал) і повертаєш її разом з нарахованими відсотками за кожен період.

Якщо ти переглянеш наші розрахунки, то побачиш, що накопичені суми на кінець кожного року мають такий вигляд:

Перший рік: $A_1=1000(1+0,1⋅1)$ , чи $A_1=P⋅(1+r)^1$ .

Другий рік: $A_2=1000(1+0,1⋅1)^2$ , чи $A_2=P⋅(1+r)^2$ .

Третій рік: $A_3=1000(1+0,1⋅1)^3$ , чи $A_3=P⋅(1+r)^3$ .

Ці спостереження наводять нас на думку про наступний загальний результат: якщо 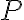$P$ доларів інвестовано протягом 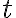$t$ років з річною складною відсотковою ставкою 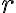$r$ (у десятковому вигляді), то загальна сума обчислюється за формулою:

$A=P⋅(1+r)^t$

Ця формула була отримана з припущенням, що відсотки нараховуються щорічно. Однак на практиці відсотки зазвичай нараховуються більше одного разу на рік. Інтервал часу між послідовними розрахунками відсотків називається періодом конвертації.

Якщо відсотки нараховуються 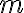$m$ разів на рік, то проста відсоткова ставка за кожний період конвертації 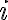$i$ дорівнює $\frac{r}{m}$ .

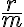Наприклад, якщо номінальна відсоткова ставка становить 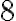$8$ % на рік ( 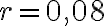$r = 0,08$ ), і відсотки нараховуються щокварталу ( 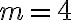$m = 4$ ), тоді проста відсоткова ставка за кожен період дорівнює 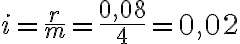$i=\frac{r}{m}=\frac{0,08}{4}=0,02$ , тобто $2$ %.

Тепер, застосовуючи цю формулу, можемо знайти загальну суму накопиченого капіталу 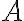$A$ після закінчення інвестиційного періоду або погашення кредиту з урахуванням складного відсотка. Загальна сума обчислюється за формулою:

$A=P \cdot(1+i)^n$

де $i=\frac{r}{m}$ , $n=mt$ , а

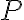$P$ — початковий капітал (сума вкладу або кредиту);

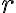$r$ — номінальна річна відсоткова ставка;

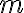$m$ — кількість періодів конвертації на рік;

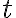$t$ — кількість років, на які ти інвестуєш гроші або береш кредит.

Ця формула допоможе зрозуміти, якою буде загальна сума накопиченого капіталу після закінчення інвестиційного періоду або погашення кредиту, з урахуванням складних відсотків та їх частоти нарахування.

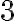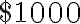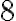Наприклад, наведена таблиця показує, якою буде загальна сума через $3$ роки при інвестуванні $$1000$ під $8$ % річних за різними періодами перерахування відсотків. Чим частіше перераховується відсоток, тим більшою є загальна сума.

Річна відсоткова ставка, $r$

Період

перерахування, $m$

Проста відсоткова ставка, $i$

Сума інвестиції, $P$

Загальна сума, $A$

8 %

Щорічно, m = 1

8 %

$1000

$1259,71

8 %

Піврічно, m = 2

4 %

$1000

$1265,32

8 %

Квартально, m = 4

2 %

$1000

$1268,24

8 %

Щомісячно, m = 12

2/3 %

$1000

$1270,24

8 %

Щоденно, m = 365

8/365 %

$1000

$1271,22

Це дуже важливо під час планування фінансових рішень, оскільки підвищена частота нарахування відсотків може значно змінити розмір твоїх накопичень або боргових зобов’язань.

_{Текст розробила Наталія Дубей}
_{з використанням ChatGPT-3.5.}

Метод оцінювання: Краща оцінка.