Квадратні нерівності з однією змінною
Квадратні нерівності — це нерівності, які містять квадратні вирази. Тобто нерівності виду 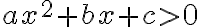 ,
, 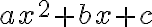 ,
, 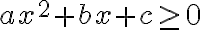 та
та 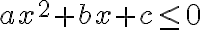 , де
, де  — змінна,
— змінна,  ,
,  і
і 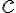 — деякі числа, причому
— деякі числа, причому 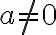 , є квадратними нерівностями.
, є квадратними нерівностями.
Як розв’язувати квадратні нерівності з однією змінною?
Крок 1: Упорядкуй нерівність
На цьому кроці переконайся, що нерівність упорядкована, тобто всі наявні доданки знаходяться з лівого боку від знака нерівності, а з правого боку знаходиться тільки нуль. Наприклад, перетворимо нерівність 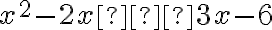 на
на 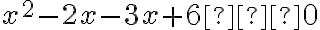 .
.
Крок 2: Спрости нерівність
На цьому кроці зведи подібні доданки в обох частинах нерівності. Після зведення подібних доданків твоя нерівність буде записана у стандартному вигляді, тобто у вигляді 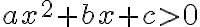 (або
(або 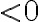 ,
,  ,
,  ). Повернувшись до нашого прикладу, отримаємо:
). Повернувшись до нашого прикладу, отримаємо: 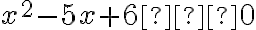 .
.
Крок 3: Знайди корені відповідного квадратного рівняння
На цьому кроці поміняй знак нерівності на знак рівності та розв’яжи відповідне квадратне рівняння 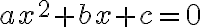 . Це можна зробити за допомогою дискримінанта
. Це можна зробити за допомогою дискримінанта 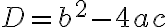 :
:
- Якщо
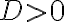 , то рівняння має два різні корені:
, то рівняння має два різні корені: 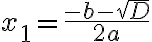 та
та 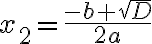 ;
; - Якщо
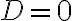 , то рівняння має один дійсний корінь:
, то рівняння має один дійсний корінь: 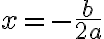 ;
; - Якщо
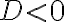 , рівняння не має дійсних коренів, що означає, що квадратичний вираз завжди додатний або завжди від’ємний.
, рівняння не має дійсних коренів, що означає, що квадратичний вираз завжди додатний або завжди від’ємний.
У нашому прикладі нам потрібно розв’язати рівняння 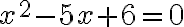 . Дискримінант даного рівняння
. Дискримінант даного рівняння 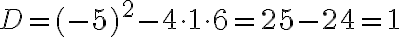 , що означає, що рівняння має два корені. Скориставшись формулою коренів квадратного рівняння, отримаємо
, що означає, що рівняння має два корені. Скориставшись формулою коренів квадратного рівняння, отримаємо 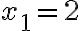 і
і 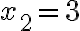 .
.
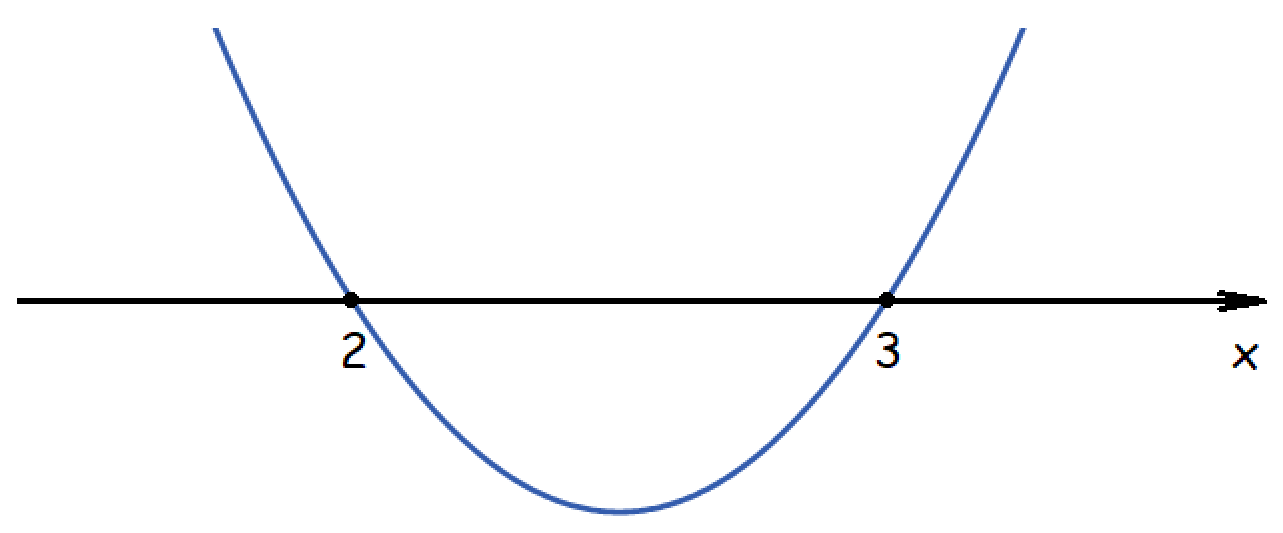
Крок 4: Побудуй схематичний графік параболи
На цьому кроці познач знайдені корені квадратного рівняння на координатній прямій та побудуй схематично параболу, яка проходитиме через знайдені корені. Нагадаємо, що якщо 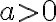 , то парабола «посміхається» (гілки напрямлені вгору), а якщо
, то парабола «посміхається» (гілки напрямлені вгору), а якщо 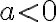 , то парабола «сумує» (гілки напрямлені вниз). Зауважимо, що у випадку, коли квадратне рівняння не має розв’язків, ти не зможеш позначити корені на числовій прямій (бо їх немає), але ти зможеш побудувати параболу. У такому випадку ця парабола не буде перетинати числову вісь.
У нашому випадку потрібно позначити на числовій прямій точки
, то парабола «сумує» (гілки напрямлені вниз). Зауважимо, що у випадку, коли квадратне рівняння не має розв’язків, ти не зможеш позначити корені на числовій прямій (бо їх немає), але ти зможеш побудувати параболу. У такому випадку ця парабола не буде перетинати числову вісь.
У нашому випадку потрібно позначити на числовій прямій точки 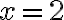 і
і 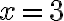 та провести через ці точки параболу вітками вгору, оскільки коефіцієнт при
та провести через ці точки параболу вітками вгору, оскільки коефіцієнт при 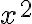 є додатним.
є додатним.
Крок 5: Запиши розв’язок нерівності
Після того, як ти побудував(-ла) схематичне зображення параболи, тобі залишається правильно прочитати розв’язки нерівності з твого рисунка і записати відповідь. Для цього врахуй, що в точках на числовій прямій значення квадратного тричлена дорівнює нулю, вище числової прямої квадратний тричлен є додатним, а нижче — від’ємним.
Дотримуйся цих кроків під час розв’язування квадратних нерівностей, і ти зможеш впоратися з будь-якою квадратною нерівністю. І пам’ятай, що практика має вирішальне значення, тому не зволікай і починай тренуватися вже зараз.
Пригадаємо, що ми розв’язуємо нерівність 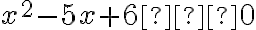 . Тому нам потрібно у відповідь записати всі значення
. Тому нам потрібно у відповідь записати всі значення  , для яких вираз
, для яких вираз 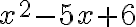 є від’ємним або дорівнює нулю, тобто ті значення
є від’ємним або дорівнює нулю, тобто ті значення  , де парабола знаходиться нижче числової прямої або де парабола перетинає числову пряму. З рисунка видно, що
, де парабола знаходиться нижче числової прямої або де парабола перетинає числову пряму. З рисунка видно, що ![x \in [2, 3] x \in [2, 3]](https://lms.smart-osvita.org/filter/tex/pix.php/5c266938be41a31e05fd7fff253c3d58.gif) , що і є розв’язком нашої нерівності.
, що і є розв’язком нашої нерівності.
Текст розробила Грибель Ольга з використанням ChatGPT-4.0.
Картинку до тексту створила Грибель Ольга в Paint.
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour