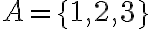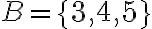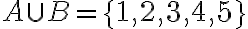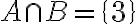Об’єднання та перетин множин
Цей мем дотепний, бо використовує відоме обличчя для демонстрації понять об’єднання та перетину множин. Навіть якщо тебе це не розсмішило, ти все одно можеш оцінити мем завдяки його простому та витонченому способу візуалізації абстрактних математичних операцій у контексті реального світу.
Тепер перейдемо до теорії множин.
Теорія множин — фундамент математики.
Множина — це набір об’єктів певної природи. Ці об’єкти ми називаємо елементами множини. Кожен елемент або належить множині, або їй не належить.
На перший погляд, поняття множини здається дуже простим та несуперечливим. Так, напевно, гадав і Георг Кантор — засновник теорії множин, допоки інший математик, Бертран Рассел, не прийшов до суперечності. Не будемо вкопуватися в математичні деталі цього парадоксу, оскільки він занадто абстрактний. Розглянемо його сюжетний аналог у вигляді задачі, над якою рекомендуємо тобі поміркувати! Отже, в містечку живе один перукар, який стриже всіх, хто сам себе не стриже. Питання: чи стриже себе перукар?
Основна ідея Кантора полягала у вивченні нескінченних множин та їхніх властивостей, що привело до відкриття різних рівнів нескінченності. Це було революційним кроком у математиці, оскільки раніше нескінченність розглядалася як абстрактне поняття без строгої математичної основи.
Кантор зіткнувся з багатьма проблемами та критикою під час розробки своєї теорії. Його робота привела до значних суперечок серед математиків того часу, але врешті-решт вона стала основою для сучасної теорії множин.
Надалі ми часто використовуватимемо множини для групування об’єктів за певними властивостями. Наприклад, множинами чисел, що є розв’язками рівняння чи нерівності, або колекцією чого б ти там не збирав (так-так, колекція — це теж множина 😉).
Давай розглянемо ще кілька прикладів множин:
- Множина всіх літер українського алфавіту:
{а, б, в, г, ґ, д, е, є, ж, з, и, і, ї, й, к, л, м, н, о, п, р, с, т, у, ф, х, ц, ч, ш, щ, ь, ю, я}
- Множина днів тижня:
{понеділок, вівторок, середа, четвер, п’ятниця, субота, неділя}
- Множина планет Сонячної системи:
{Меркурій, Венера, Земля, Марс, Юпітер, Сатурн, Уран, Нептун}
- Множина книг, які варто прочитати:
{1984, За Перекопом є земля, Колонія, Гаррі Поттер, Навчитися вчитися, Зазирни у мої сни}
Об’єднання множин
Об’єднання множин — це операція, яка об’єднує всі елементи двох або більше множин в одну нову множину. Елементи в новій множині не повторюються.
Наприклад, якщо є дві множини:
Тоді об’єднання множин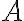 
і 
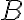буде:
Перетин множин
Перетин множин — це операція, яка знаходить спільні елементи двох або більше множин і створює нову множину з цих спільних елеменів.
Наприклад, якщо є дві множини:
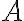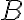Тоді перетин множин і буде:
Давай розглянемо ще більше прикладів.
Об’єднання множин. Припустимо, у тебе є два списки друзів: один із соціальних мереж та інший — зі школи. Об’єднання цих двох множин створить один великий список друзів, у якому будуть всі люди з обох списків.
Перетин множин. Припустимо, у тебе є дві групи друзів: ті, кого ти запрошуєш на свою вечірку, і ті, хто любить піцу. Перетин цих двох множин дасть тобі список друзів, яких ти можеш запросити на вечірку з піцою. Таким чином, ти зможеш врахувати інтереси своїх друзів під час планування вечірки.
Ці операції посідають важливе місце у реальному світі, особливо в ситуаціях, коли нам потрібно робити вибір на основі декількох факторів. Вони допомагають нам організовувати інформацію та приймати виважені рішення.
Чи любиш ти колекціонувати речі? Можливо, ти збираєш поштові марки, наклейки, пластикові фігурки з фастфудів або, можливо, навіть шоколадні обгортки? Якщо так, то ти вже знайомий з поняттям підмножини, навіть якщо ти про це не здогадувався.
Давай уявимо, що у тебе є велика колекція книг. Це твоя множина. Тепер візьми лише ті книги, що були написані твоїм улюбленим автором. Це вже підмножина твоєї великої множини книг. Чи ще один приклад: уяви усіх своїх друзів (це буде множина), а тепер виділи тільки тих, хто ходить з тобою в один клас — це буде підмножина.
Отже, наступного разу, коли ти будеш сортувати свої речі, пам’ятай: ти використовуєш математичний принцип підмножин!
Вивчення теорії множин надає нам інструменти для ефективної роботи з групами об’єктів, виконання операцій над ними та отримання висновків про їхні властивості.
Теорію розробив Чоп’юк Юрій з використанням ChatGPT
Картинки взято з мережі
Метод оцінювання: Краща оцінка.