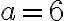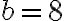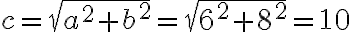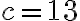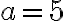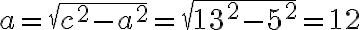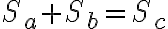Теорема Піфагора
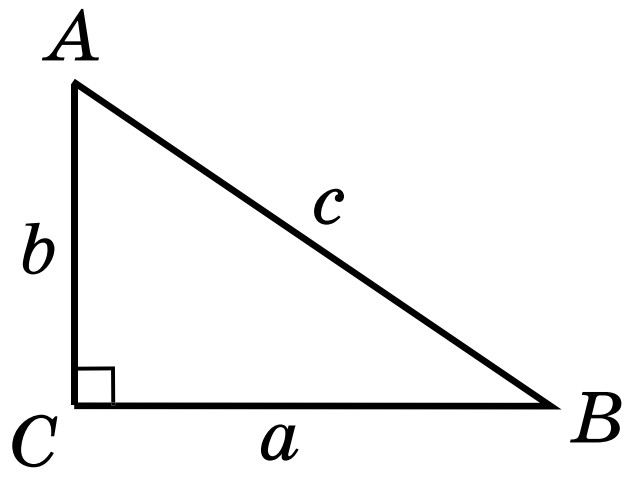
Теорема Піфагора. У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.
Якщо позначити в 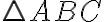 (
(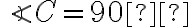 )
) 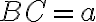 ,
, 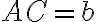 ,
, 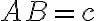 , то
, то
теорему Піфагора можна записати формулою:
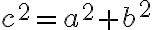 .
.
Теорема Піфагора — одна з найцікавіших і найважливіших теорем геометрії.
За допомогою теореми Піфагора, знаючи дві сторони прямокутного трикутника, можна знайти третю.
У цьому нам допоможе така схема:
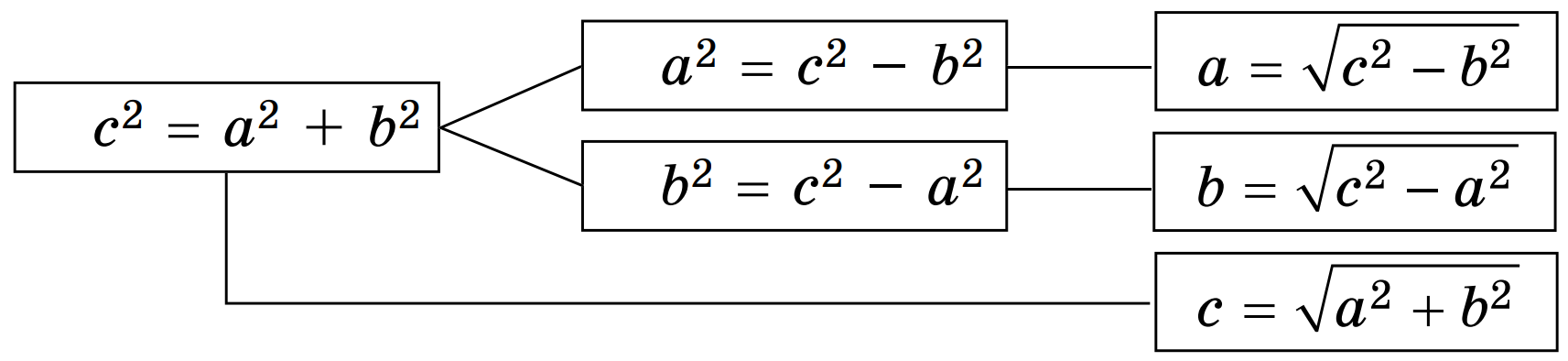
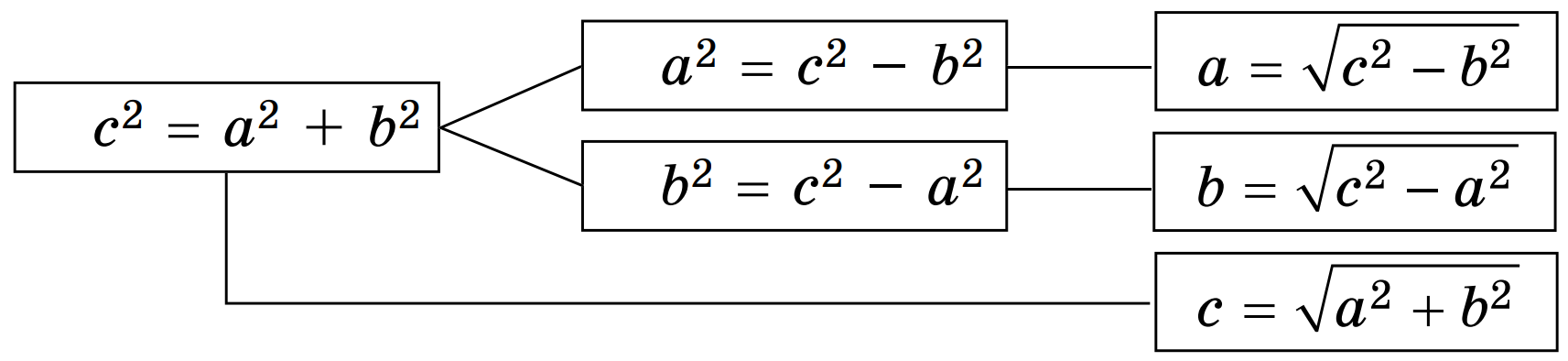
Скориставшись цими формулами, за двома будь-якими сторонами прямокутного трикутника можна знайти його третю сторону.
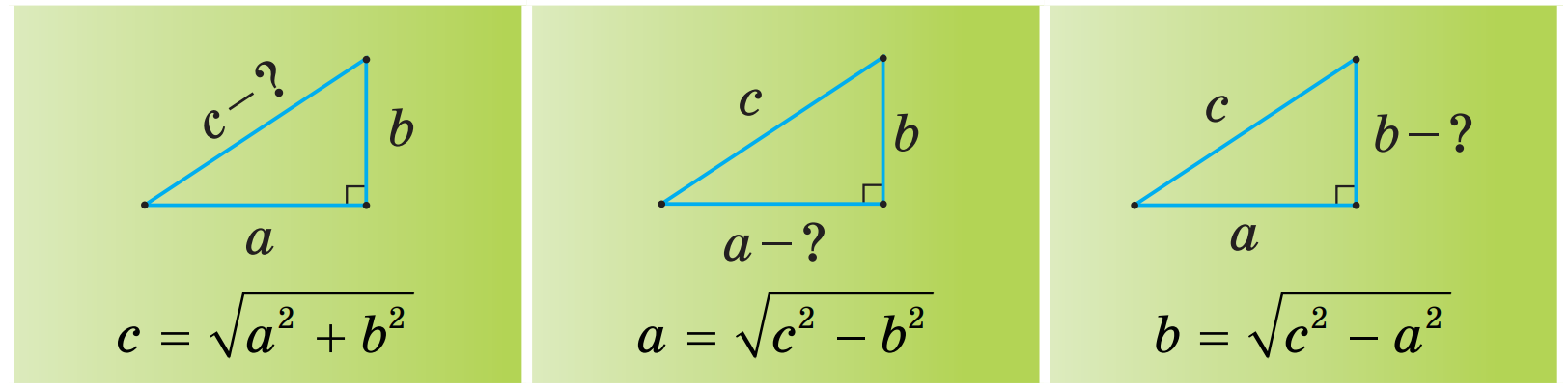
Наприклад:
Правильною є і теорема, обернена до теореми Піфагора: якщо квадрат сторони трикутника дорівнює сумі квадратів двох інших його сторін, то цей трикутник — прямокутний.
За теоремою, оберненою до теореми Піфагора, трикутник зі сторонами 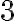 см,
см, 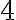 см і
см і 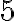 см — прямокутний, оскільки
см — прямокутний, оскільки 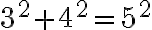 . Прямокутний трикутник із такими сторонами називають єгипетським, оскільки вважається, що його використовували у Давньому Єгипті для побудови прямих кутів на місцевості.
. Прямокутний трикутник із такими сторонами називають єгипетським, оскільки вважається, що його використовували у Давньому Єгипті для побудови прямих кутів на місцевості.
Трійку цілих чисел, що задовольняє теорему Піфагора, називають піфагоровою трійкою чисел, а трикутник, для якого вона є довжинами сторін, — піфагоровим трикутником.
Наприклад, піфагоровою є не тільки трійка чисел 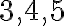 , а й далі в порядку зростання чисел ідуть такі
піфагорові трійки:
, а й далі в порядку зростання чисел ідуть такі
піфагорові трійки: 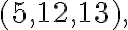
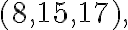
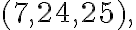
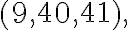
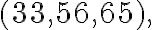
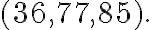
Зауважимо, що з теореми Піфагора та теореми, оберненої до неї, випливає, що трикутник є прямокутним тоді й тільки тоді, коли квадрат найбільшої сторони трикутника дорівнює сумі квадратів двох інших його сторін.
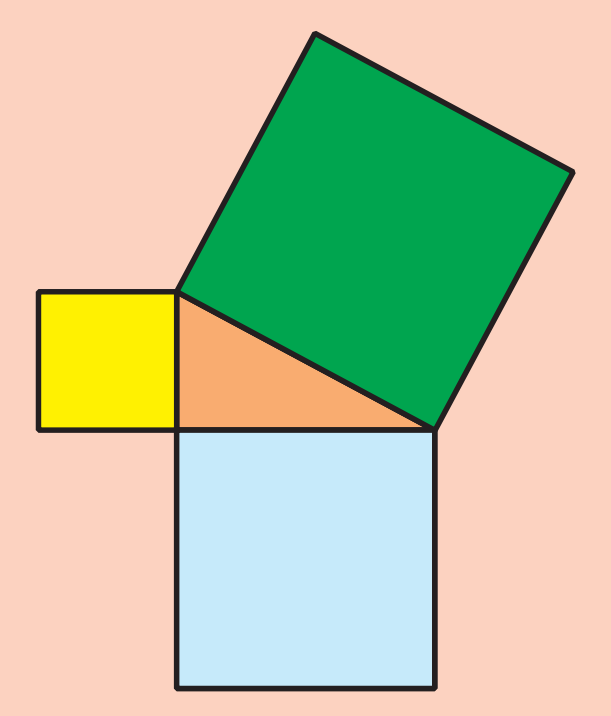 З урахуванням того, що числом
З урахуванням того, що числом 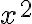 виражається площа квадрата зі стороною
виражається площа квадрата зі стороною  , теорему Піфагора можна сформулювати так: сума площ квадратів, побудованих на катетах прямокутного трикутника, дорівнює площі квадрата, побудованого на гіпотенузі.
, теорему Піфагора можна сформулювати так: сума площ квадратів, побудованих на катетах прямокутного трикутника, дорівнює площі квадрата, побудованого на гіпотенузі.
Багато поколінь школярів і школярок називають геометричну фігуру, яка ілюструє цей факт, «Піфагорові штани» й формулюють теорему в жартівливій формі: «Піфагорові штани на всі сторони рівні».
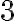 см,
см, 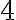 см і
см і 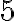 см — прямокутний, оскільки
см — прямокутний, оскільки 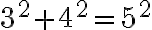 . Прямокутний трикутник із такими сторонами називають єгипетським, оскільки вважається, що його використовували у Давньому Єгипті для побудови прямих кутів на місцевості.
. Прямокутний трикутник із такими сторонами називають єгипетським, оскільки вважається, що його використовували у Давньому Єгипті для побудови прямих кутів на місцевості.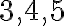 , а й далі в порядку зростання чисел ідуть такі
піфагорові трійки:
, а й далі в порядку зростання чисел ідуть такі
піфагорові трійки: 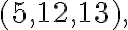
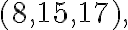
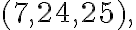
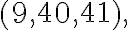
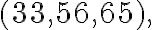
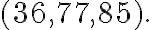
 З урахуванням того, що числом
З урахуванням того, що числом 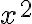 виражається площа квадрата зі стороною
виражається площа квадрата зі стороною  , теорему Піфагора можна сформулювати так: сума площ квадратів, побудованих на катетах прямокутного трикутника, дорівнює площі квадрата, побудованого на гіпотенузі.
, теорему Піфагора можна сформулювати так: сума площ квадратів, побудованих на катетах прямокутного трикутника, дорівнює площі квадрата, побудованого на гіпотенузі.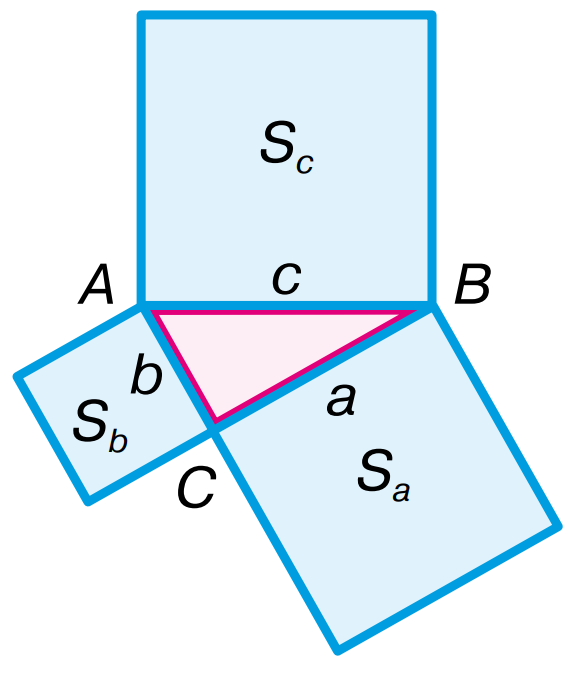
Джерела:
1. О.С. Істер. Геометрія: підручник для 8-го класу. 2021 рік. Шкільні підручники онлайн. URL: https://pidruchnyk.com.ua/804-geometriya-8-klas-ister-2016.html
2. Г. П. Бевз, В. Г. Бевз, Н. Г. Владімірова. Геометрія: підручник для 8-го класу. 2021 рік. Шкільні підручники онлайн. URL: https://pidruchnyk.com.ua/859-geometriya-8-klas-bevz-vladmrova-2016.html
3. М.І. Бурда, Н.А. Тарасенкова. Геометрія: підручник для 8-го класу. 2021 рік. Шкільні підручники онлайн. URL: https://pidruchnyk.com.ua/834-geometriya-burda-tarasenkova-8-klas.html
4. В.О Тадеєв. Геометрія: підручник для 8-го класу. 2016 рік. Шкільні підручники онлайн. URL: https://pidruchnyk.com.ua/835-geometriya-8-klas-tadeev.html
5. А.Г. Мерзляк, В.Б. Полонський,
М.С. Якір. Геометрія: підручник для 8-го класу. 2021 рік. Шкільні підручники онлайн. URL: https://pidruchnyk.com.ua/796-merzlyak-2016-geometriya-8-klas.html
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour