Обернена пропорційність, її графік та властивості
Пригадаємо, що залежність, за якої при збільшенні (зменшенні) однієї величини у кілька разів друга величина зменшується (збільшується) у таку саму кількість разів, називається оберненою пропорційністю.
Розглянемо декілька прикладів.
ПРИКЛАД 1. Припустимо, що у нас є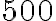 
гривень. Позначимо через 
грн ціну 1 кг товару, а через 
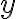кг — кількість цього товару, яку можна придбати за 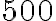грн. Залежність між 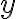і є оберненою пропорційністю: збільшення ціни у кілька разів призводить до зменшення кількості товару в ту саму кількість разів, і навпаки, зменшення ціни призводить до збільшення кількості товару. Цій функціональній залежності відповідає функція, задана формулою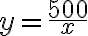 
.
ПРИКЛАД 2. Уявімо, що ми вирушаємо в подорож у сусіднє місто, відстань до якого 73 км. Чим більша швидкість руху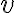 
, тим менше часу 
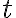нам знадобиться для подолання відстані.
Ця залежність також є оберненою пропорційністю. Їй відповідає формула: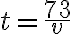 
.
У розглянутих прикладах математичною моделлю реальних ситуацій є функція, яку можна задати формулою виду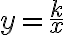 
. Таку функцію називають оберненою пропорційністю (кутовий коефіцієнт 
).
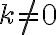Залежно від знака кутового коефіцієнта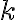 
графік набуває одного з виглядів:
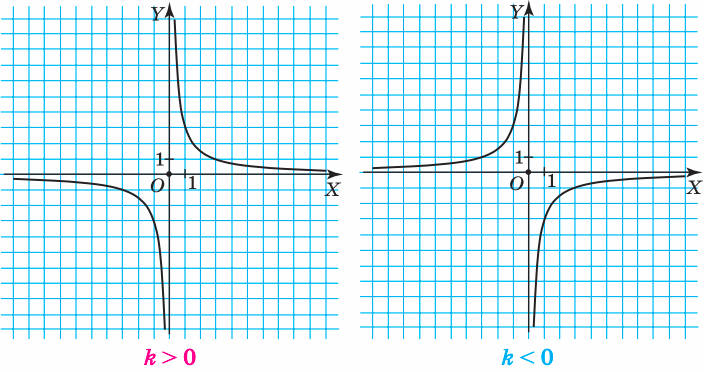
Фігуру, яка є графіком функції 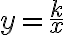, де 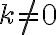, називають гіперболою.
Із графіків легко побачити, що виконується:
Розглянь наступну таблицю, яка містить ще деякі властивості функції .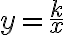
Теорію впорядкувала Савчин Марія
Джерела:
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour