Числові нерівності


На практиці ми часто порівнюємо різні величини. Наприклад, площа Австралії (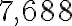 млн км²) більша за площу Індії (
млн км²) більша за площу Індії (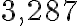 млн км²), висота Ейфелевої вежі (
млн км²), висота Ейфелевої вежі (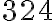 м) більша за висоту Піраміди Хеопса (
м) більша за висоту Піраміди Хеопса (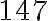 м).
м).
Результати таких порівнянь можна записувати у вигляді числових нерівностей, використовуючи знаки 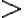 та
та 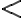 . Зокрема, якщо число
. Зокрема, якщо число 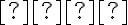 більше за число
більше за число 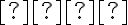 , то пишуть
, то пишуть 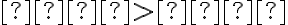 , а якщо число
, а якщо число 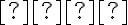 менше за число
менше за число 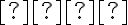 , то пишуть
, то пишуть 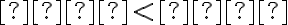 .
.
Зауважимо, що число 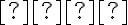 вважають більшим за число
вважають більшим за число 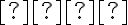 , якщо різниця
, якщо різниця 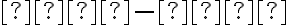 є додатним числом. Число
є додатним числом. Число 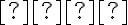 вважають меншим за число
вважають меншим за число 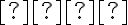 , якщо різниця
, якщо різниця 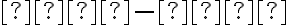 є від’ємним числом.
є від’ємним числом.
Зрозуміло, що різниця чисел  і
і  може бути або додатною, або від’ємною, або рівною
нулю, тому для будь-яких чисел
може бути або додатною, або від’ємною, або рівною
нулю, тому для будь-яких чисел  і
і  справедливе одне і тільки одне з таких співвідношень:
справедливе одне і тільки одне з таких співвідношень: 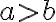 ,
, 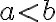 ,
, 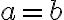 .
.
Часто в повсякденному житті ми користуємося висловами «не більше ніж», «не менше ніж». Наприклад, відповідно до санітарних норм кількість учнів у класі має бути не більшою ніж 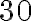 .
.
У математиці для вислову «не більше ніж» використовують знак 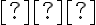 (читають: «менше або дорівнює»), а для вислову «не менше ніж» — знак
(читають: «менше або дорівнює»), а для вислову «не менше ніж» — знак 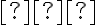 (читають: «більше або дорівнює»).
(читають: «більше або дорівнює»).
Знаки  і
і 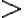 називають знаками строгої нерівності, а знаки
називають знаками строгої нерівності, а знаки 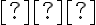 і
і 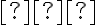 називають знаками нестрогої нерівності.
називають знаками нестрогої нерівності.
Основні властивості числових нерівностей:
- Якщо
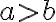 і
і 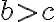 , то
, то 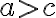 .
. - Якщо
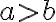 і
і 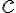 — будь-яке число, то
— будь-яке число, то 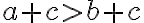 .
. - Якщо
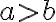 і
і 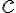 — додатне число, то
— додатне число, то 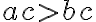 .
. - Якщо
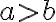 і
і 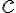 — від’ємне число, то
— від’ємне число, то 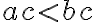 .
. - Якщо
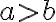 і
і 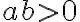 , то
, то 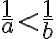 .
.
Аналогічні властивості притаманні й нестрогим нерівностям. Це означає, що якщо поміняти 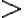 на
на 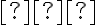 , а
, а 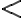 на
на 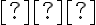 , то всі властивості працюватимуть.
, то всі властивості працюватимуть.
Джерело: Алгебра: підруч. для 9 кл. загальноосвіт. навч. закладів / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. — Х. : Гімназія, 2017. — 272 с. : іл. ISBN 978-966-474-293-8. URL: https://files.pidruchnyk.com.ua/uploads/book/9_klas_algebra_merzljak_2017.pdf
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour