Локальні екстремуми_к
Поняття локального екстремуму має численні застосування в бізнесі, економіці, техніці. Давай наведемо деякі з важливих застосувань.
- Ціна акції, представлена у вигляді функціонального рівняння та графіка, допоможе знайти точки, де ціна акції є максимальною та мінімальною.
- Напругу в електроприладі, при якій вона досягає піку, можна визначити за допомогою максимумів функції напруги.
- У харчових установках вологість представлена функцією, і максимальну вологість, при якій харчові продукти псуються, і мінімальну вологість, необхідну для збереження харчових продуктів свіжими, можна знайти з екстремумів.
- Кількість насіння, яке потрібно висіяти на полі для отримання максимального врожаю, можна знайти з максимумів функції.
- Знаючи максимуми, можна знайти максимальну висоту, якої досягає м’яч, що підкинутий у повітря і рухається по параболічній траєкторії.
Що, якби ми сказали тобі, що за рівнянням функції ти можеш знайти всі-всі точки її локального максимуму та мінімуму? І це правда!
Точка локального максимуму — це точка, де функція змінює напрямок від зростання до спадання (роблячи цю точку «піком» на графіку).
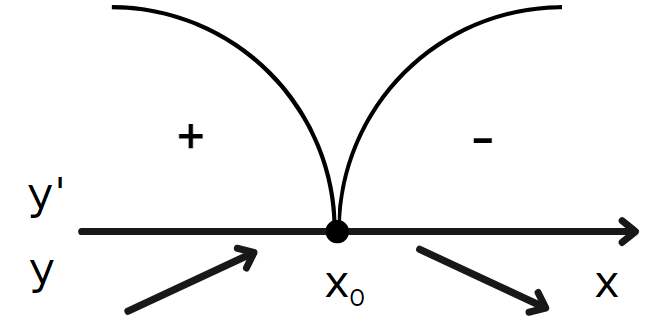
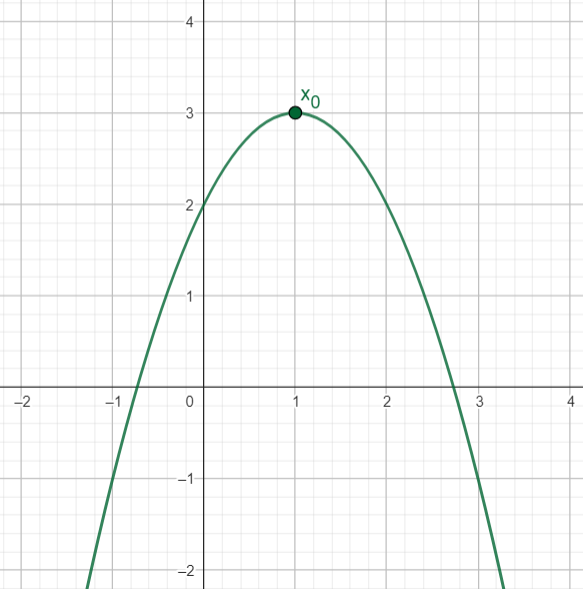
Подібним чином точка локального мінімуму — це точка, де функція змінює напрямок від спадання до зростання (роблячи цю точку «низом» на графіку).
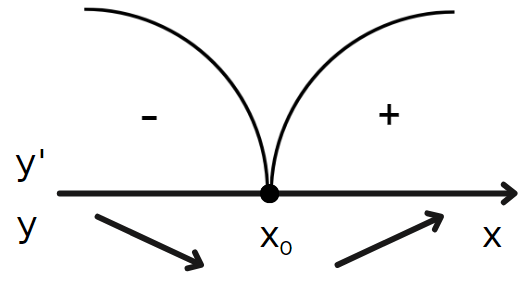
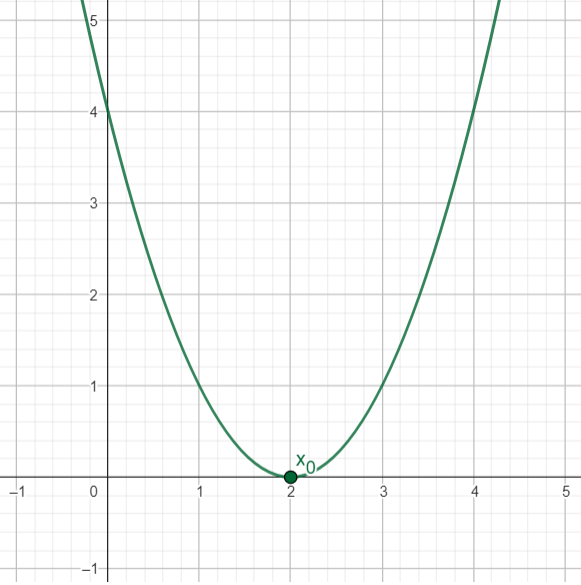
Якщо зміни знаків не відбулося, то така точка не є точкою локального екстремуму.
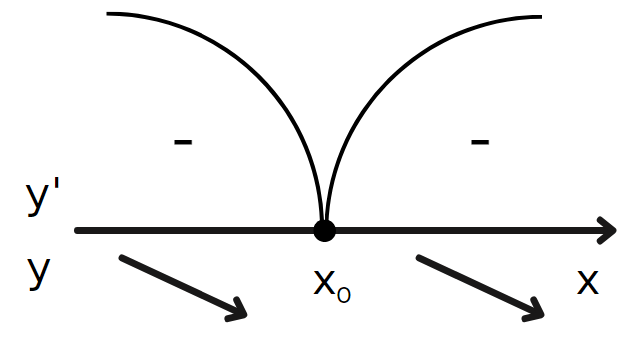
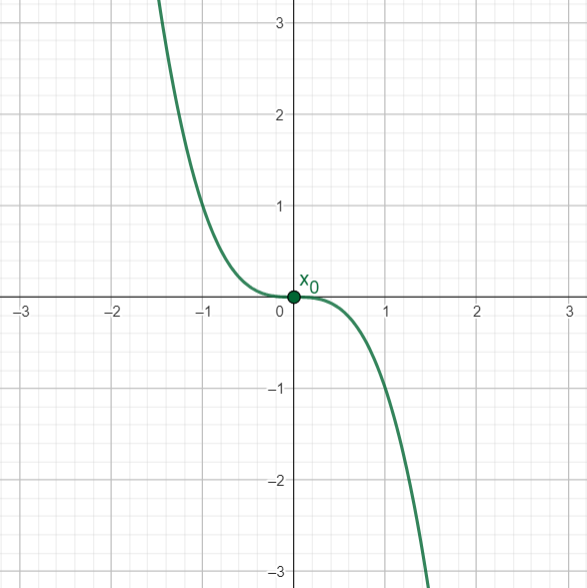
Точки локального максимуму і мінімуму разом називають точками локального екстремуму, а значення функції у цих точках — локальними екстремумами функції.
Ти вже знаєш, як знайти проміжки зростання та спадання функції. Пошук точок локального екстремуму передбачає ще один крок: пошук точок, де функція змінює напрямок. Точками локального екстремуму функції можуть бути тільки її критичні точки. Тому, шукаючи точки локального екстремуму функції, у першу чергу треба знайти її критичні точки. Але пам’ятати, що не кожна критична точка є точкою екстремуму.
Розглянемо приклад. М’яч підкинуто в повітря. Його висота в будь-який момент часу 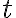 визначається як
визначається як
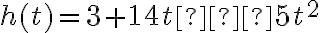 .
.
Яка його максимальна висота?
Розв’язання. 1. Знайдемо область визначення функції: 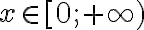 .
.
2. Знайдемо похідну 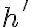 функції
функції 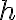 :
: 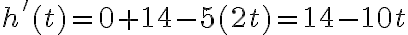 .
.
3. Знайдемо критичні точки функції: 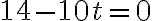 . Таким чином,
. Таким чином, 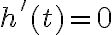 , коли
, коли 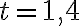 .
.
4. Поділимо знайденою критичною точкою область визначення функції на проміжки. Отримаємо: ![[0;~ 1,4] \cup [1,4;~+ \infty) [0;~ 1,4] \cup [1,4;~+ \infty)](https://lms.smart-osvita.org/filter/tex/pix.php/482e42e6b2f6e5f91ebdf91609a1911e.gif) .
.
5. Позначимо критичну точку на числовій прямій, визначимо, чи точка є точкою екстремуму і якою саме, максимуму чи мінімуму.
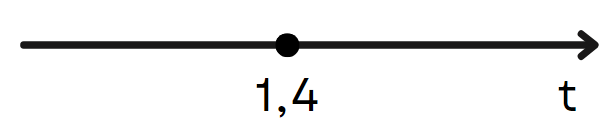
Спочатку з’ясуємо знак похідної на вказаних проміжках. Підставимо точку з першого проміжку в рівняння похідної. Наприклад, 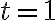 , будемо мати
, будемо мати 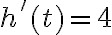 . Підставимо точку з другого проміжку в рівняння похідної. Наприклад,
. Підставимо точку з другого проміжку в рівняння похідної. Наприклад, 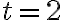 , будемо мати
, будемо мати 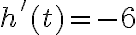 . Отже,
. Отже, 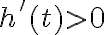 для
для 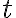 в інтервалі
в інтервалі ![[0;~ 1,4] [0;~ 1,4]](https://lms.smart-osvita.org/filter/tex/pix.php/847f0953766351a09596573c9f4b1382.gif) , а
, а 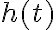
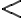
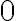 для
для  в інтервалі
в інтервалі 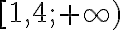 .
.
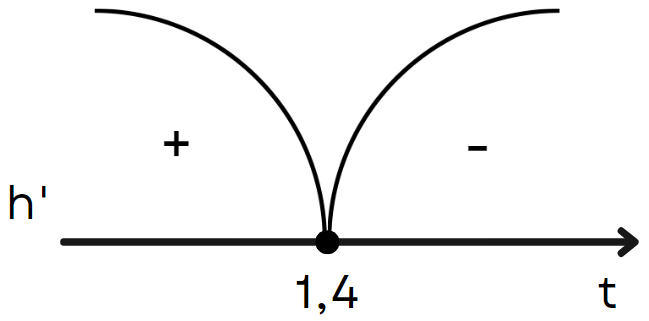
Це означає, що функція 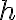 зростає на
зростає на ![[0;~ 1,4] [0;~ 1,4]](https://lms.smart-osvita.org/filter/tex/pix.php/847f0953766351a09596573c9f4b1382.gif) і спадає на
і спадає на 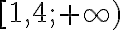 .
.
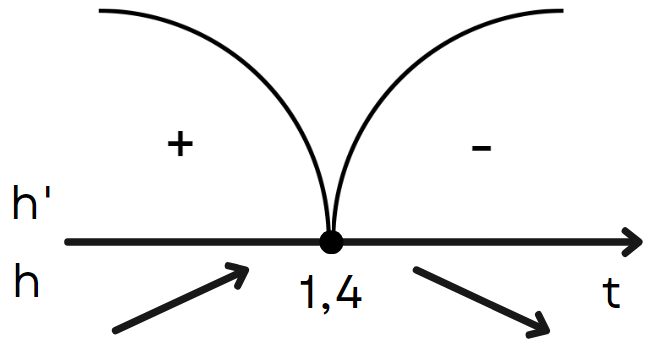
Отже, точка 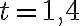 є точкою локального максимуму. Тепер можемо знайти максимальну висоту, на яку було підкинуто м’яч:
є точкою локального максимуму. Тепер можемо знайти максимальну висоту, на яку було підкинуто м’яч: 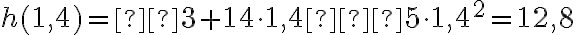 метрів.
метрів.
У кінці для наочності і розуміння, чи роз’язок правильний, глянемо на графік функції.
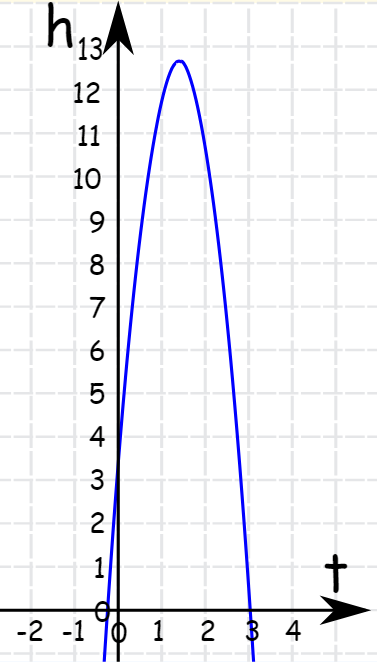
Все добре!
Теорію впорядкувала Луців Ілона-Анна.
Джерела:
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour