Розпізнаємо коефіцієнти
Ти вже знаєш, що таке буквені вирази і вмієш їх спрощувати за допомогою правил додавання та множення. Наприклад, якщо ти помножиш 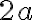 на
на 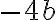 , то отримаєш
, то отримаєш 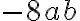 . Число
. Число 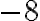 у цьому виразі називається коефіцієнтом.
у цьому виразі називається коефіцієнтом.
Тепер давай розглянемо вираз 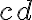 . Чи має він коефіцієнт? Так, має. Коефіцієнт дорівнює
. Чи має він коефіцієнт? Так, має. Коефіцієнт дорівнює 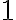 , оскільки вираз
, оскільки вираз 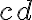 можна записати як
можна записати як 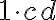 .
.
Пригадаймо також, що коли у нас є вираз із дужками, то ми можемо їх розкрити. Наприклад, до виразу 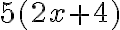 ми можемо застосувати розподільну властивість множення відносно додавання і отримати
ми можемо застосувати розподільну властивість множення відносно додавання і отримати 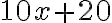 .
.
Обернена дія в цьому прикладі — це винесення спільного множника за дужки. Ми будемо використовувати винесення спільного множника за дужки при зведенні подібних доданків.
Сподіваюся, ти пам’ятаєш, що подібними називаються доданки, які містять однакові буквені множники. Наприклад, у виразі 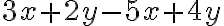 доданки
доданки 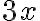 і
і 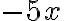 є подібними, оскільки обидва містять множник
є подібними, оскільки обидва містять множник  . Аналогічно доданки
. Аналогічно доданки 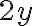 і
і 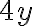 є подібними, оскільки обидва містять множник
є подібними, оскільки обидва містять множник 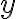 . По черзі ми складаємо подібні доданки разом і виносимо спільний множник за дужки. Наприклад, замість
. По черзі ми складаємо подібні доданки разом і виносимо спільний множник за дужки. Наприклад, замість 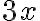 і
і 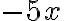 ми можемо записати
ми можемо записати 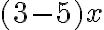 , що дорівнює
, що дорівнює 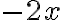 . Аналогічно замість
. Аналогічно замість 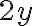 і
і 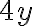 ми можемо записати
ми можемо записати 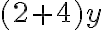 , що дорівнює
, що дорівнює 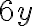 . Отже, після зведення подібних доданків у виразі
. Отже, після зведення подібних доданків у виразі 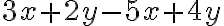 ми отримаємо вираз
ми отримаємо вираз 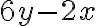 .
.
Розглянемо вираз 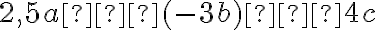 . За допомогою властивостей множення його можна спростити:
. За допомогою властивостей множення його можна спростити:
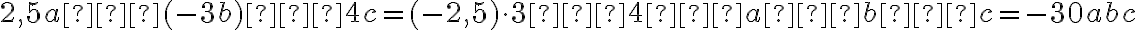 .
.
В отриманому виразі 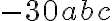 числовий множник
числовий множник 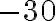 є коефіцієнтом.
є коефіцієнтом.
Розглянемо ще кілька прикладів.
У виразі 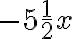 коефіцієнтом є число
коефіцієнтом є число 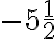 , а у виразі
, а у виразі 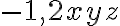 коефіцієнт дорівнює
коефіцієнт дорівнює 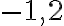 .
.
Зауважимо, що у виразі 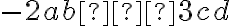 жодне із чисел
жодне із чисел 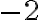 і
і 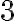 не є коефіцієнтом. У даному виразі коефіцієнт дорівнює
не є коефіцієнтом. У даному виразі коефіцієнт дорівнює 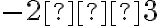 , що дорівнює
, що дорівнює 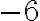 .
.
У наступних завданнях потренуйся знаходити коефіцієнт буквеного виразу.
Теорію розробила Грибель Ольга з використанням ChatGPT-3.5.
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour