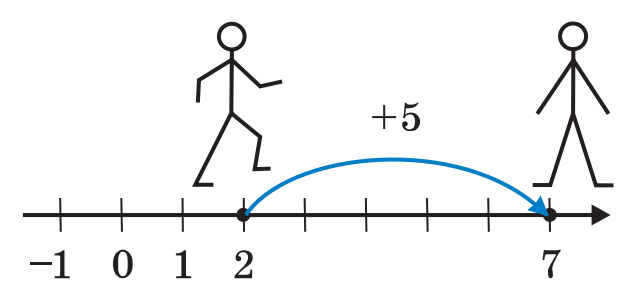
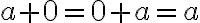Додавання раціональних чисел
Де опиниться мандрівник, який перебуває в точці з координатою  , якщо він переміститься на
, якщо він переміститься на  одиничних відрізків праворуч? Звісно, у точці з координатою
одиничних відрізків праворуч? Звісно, у точці з координатою 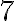 . Адже
. Адже 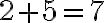 .
.
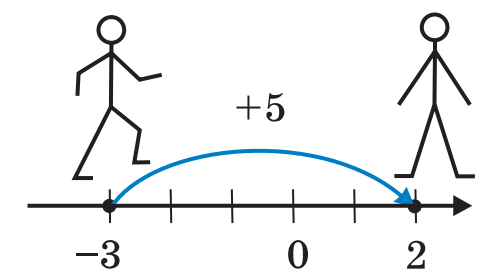
Тут ми за допомогою координатної прямої знайшли суму чисел 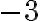 і
і  , тобто
, тобто 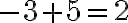 .
.
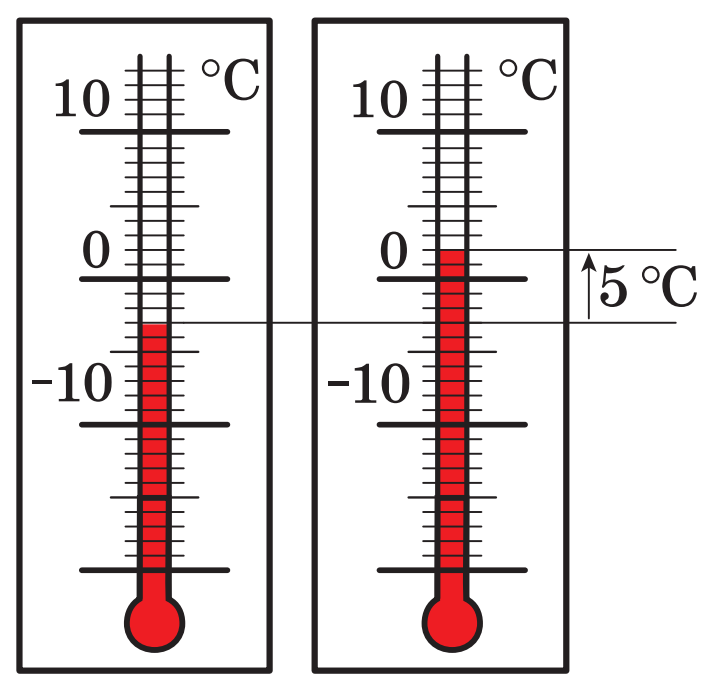
Правильність записаної рівності підтверджують і такі спостереження. Якщо температура повітря дорівнювала 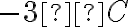 і підвищилася на
і підвищилася на 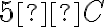 , то термометр покаже
, то термометр покаже 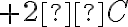 .
.
Так само зрозуміло, що, перемістившись від точки з координатою 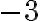 в тому самому напрямку на
в тому самому напрямку на  одиничних відрізків, він потрапить у точку з координатою
одиничних відрізків, він потрапить у точку з координатою  .
.
За допомогою координатної прямої знайдемо ще кілька сум раціональних чисел:
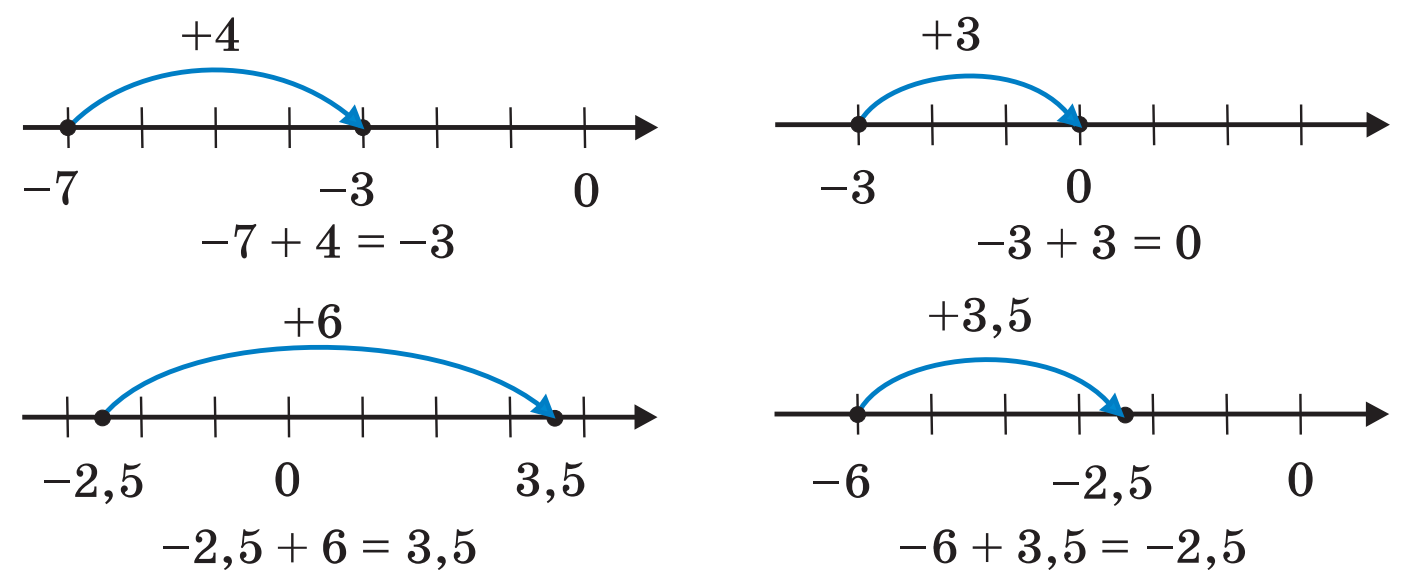
Можна помітити таку закономірність: якщо до числа  додати додатне число
додати додатне число  , то точка з координатою
, то точка з координатою  переміститься по координатній прямій на
переміститься по координатній прямій на  одиничних відрізків праворуч.
одиничних відрізків праворуч.
Цей висновок, у свою чергу, підказує таку властивість: якщо до числа  додати від’ємне число
додати від’ємне число  , то точка з координатою
, то точка з координатою  переміститься по координатній прямій на
переміститься по координатній прямій на 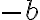 одиничних відрізків ліворуч.
одиничних відрізків ліворуч.
Наприклад, якщо до числа 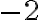 додати число
додати число 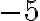 , то точка
, то точка 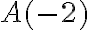 переміститься в точку
переміститься в точку 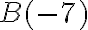 :
:
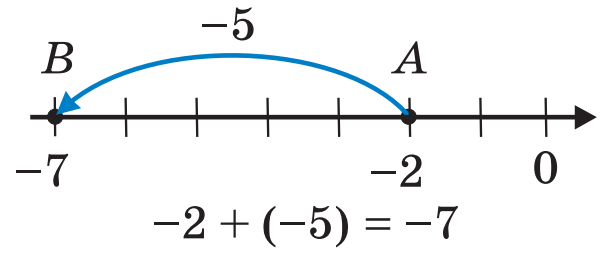
Правильність записаної рівності 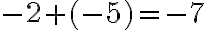 підтверджує і такий приклад. Якщо борг бізнесмена банку становив
підтверджує і такий приклад. Якщо борг бізнесмена банку становив 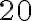 тис. грн, а він узяв у кредит ще
тис. грн, а він узяв у кредит ще 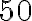 тис. грн, то залишок на його рахунку становитиме
тис. грн, то залишок на його рахунку становитиме 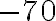 тис. грн.
тис. грн.
Розглянемо ще кілька прикладів:
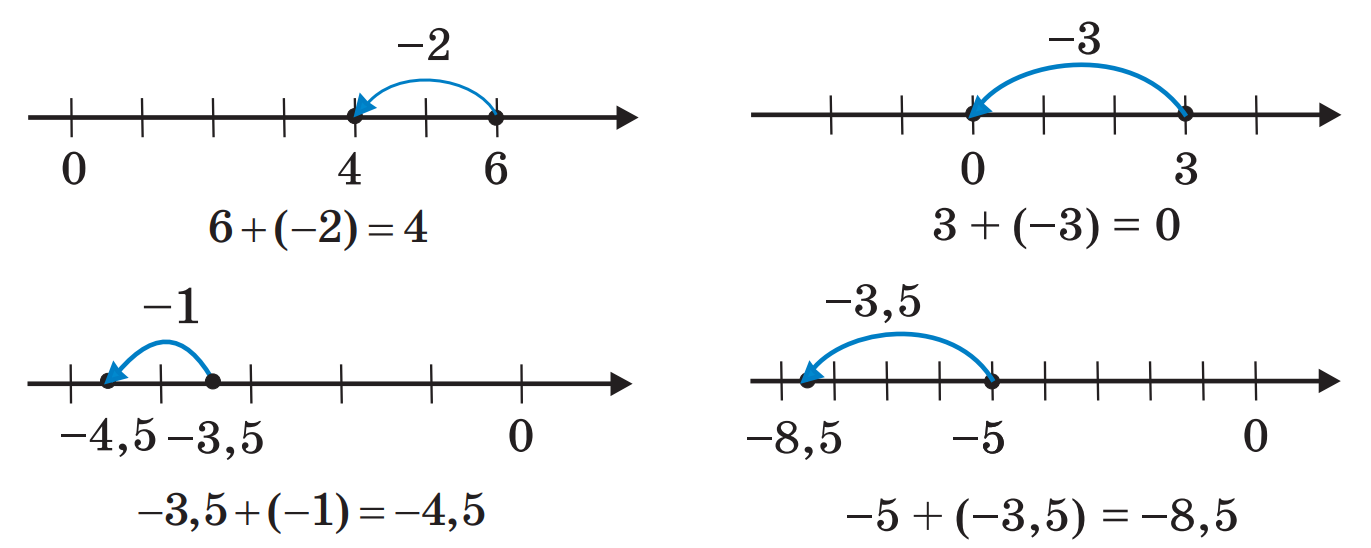
Отже, ми навчилися додавати раціональні числа за допомогою координатної прямої.
Випишемо приклади, у яких ми додавали числа з різними знаками та різними модулями:
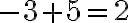 ;
; 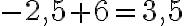 ;
; 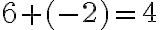 .
.
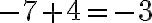 ;
; 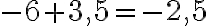 ;
;
Ці приклади ілюструють таке правило.
Щоб додати два числа з різними знаками, треба:
- знайти модулі доданків;
- від більшого модуля відняти менший модуль;
- перед отриманим числом поставити знак доданка з більшим модулем.
Тепер випишемо приклади, у яких додавали два від’ємних числа:
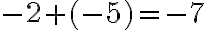 ;
;
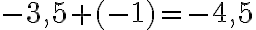 ;
;
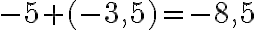 .
.
Ці приклади ілюструють таке правило.
Щоб додати два від’ємних числа, треба:
У нас залишилися ще два приклади:
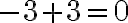 ;
;
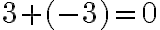 .
.
Ці приклади підказують, що справедливе таке твердження. Сума двох протилежних чисел дорівнює нулю.
.Джерело: А.Г. Мерзляк, В.Б. Полонський, М.С. Якір. Математика: підручник для 6-го класу. Частина 2. 2023 рік. Шкільні підручники онлайн. URL: https://pidruchnyk.com.ua/2589-matematyka-6-klas-merzliak-2023.html
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour