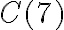Відстань між двома точками
Задача. Знайдіть відстань між точками:
Розв’язання.
- На координатній прямій позначимо точки
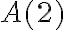 і
і 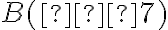 . З умови випливає, що
. З умови випливає, що 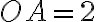 од.,
од., 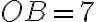 од. Оскільки точки
од. Оскільки точки 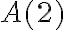 і
і 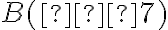 розміщуються по різні боки від точки
розміщуються по різні боки від точки  , то
, то 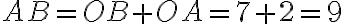 (од.). Отже, шукана відстань дорівнює сумі модулів координат даних точок.
(од.). Отже, шукана відстань дорівнює сумі модулів координат даних точок.

-
На координатній прямій позначимо точки
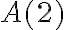 і
і 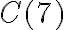 . З умови випливає, що
. З умови випливає, що 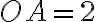 од.,
од., 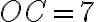 од. Оскільки точки
од. Оскільки точки 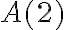 і
і 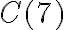 розміщуються по один бік від точки
розміщуються по один бік від точки  , то
, то 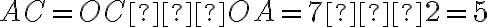 (од.). Отже, шукана відстань дорівнює різниці більшого і меншого модулів координат даних точок.
(од.). Отже, шукана відстань дорівнює різниці більшого і меншого модулів координат даних точок.

- На координатній прямій позначимо точки
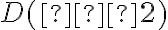 і
і 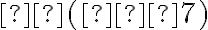 . З умови випливає, що
. З умови випливає, що 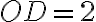 од.,
од., 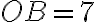 од. Оскільки точки
од. Оскільки точки 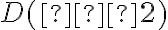 і
і 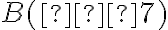 розміщуються по один бік від точки
розміщуються по один бік від точки  , то
, то 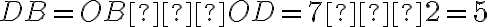 (од.). Отже, шукана відстань дорівнює різниці більшого й меншого модулів координат даних точок.
(од.). Отже, шукана відстань дорівнює різниці більшого й меншого модулів координат даних точок.

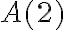 і
і 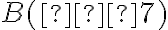 . З умови випливає, що
. З умови випливає, що 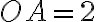 од.,
од., 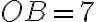 од. Оскільки точки
од. Оскільки точки 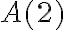 і
і 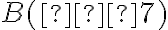 розміщуються по різні боки від точки
розміщуються по різні боки від точки  , то
, то 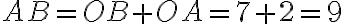 (од.). Отже, шукана відстань дорівнює сумі модулів координат даних точок.
(од.). Отже, шукана відстань дорівнює сумі модулів координат даних точок.
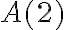 і
і 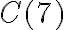 . З умови випливає, що
. З умови випливає, що 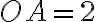 од.,
од., 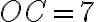 од. Оскільки точки
од. Оскільки точки 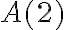 і
і 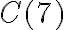 розміщуються по один бік від точки
розміщуються по один бік від точки  , то
, то 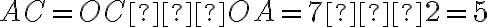 (од.). Отже, шукана відстань дорівнює різниці більшого і меншого модулів координат даних точок.
(од.). Отже, шукана відстань дорівнює різниці більшого і меншого модулів координат даних точок. 
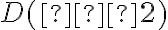 і
і 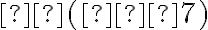 . З умови випливає, що
. З умови випливає, що 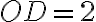 од.,
од., 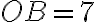 од. Оскільки точки
од. Оскільки точки 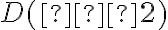 і
і 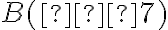 розміщуються по один бік від точки
розміщуються по один бік від точки  , то
, то 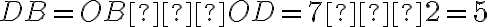 (од.). Отже, шукана відстань дорівнює різниці більшого й меншого модулів координат даних точок.
(од.). Отже, шукана відстань дорівнює різниці більшого й меншого модулів координат даних точок.
Щоб знайти відстань між двома точками за їх координатами, треба:
додати модулі координат, якщо координати мають різні знаки;
від більшого модуля координати відняти менший модуль координати, якщо координати мають однакові знаки.
Джерело: Н.А. Тарасенкова, І.М. Богатирьова, О.М. Коломієць, З.О. Сердюк. Математика: підручник для 6-го класу. 2023 рік. Шкільні підручники онлайн. URL: https://pidruchnyk.com.ua/2588-matematyka-6-klas-tarasenkova-2023.html
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour