Основні правила комбінаторики_к

Чи спадало тобі коли-небудь на думку, що тобі нічого одягнути? Якщо так, спробуй замінити запитання «що мені одягнути?» на «скількома способами я можу вибрати вбрання?». Зробивши це, ти передаш цю проблему в руки комбінаторики, і вона покаже, що варіантів вибору у тебе чимало. Ти запитаєш: «Що воно таке, ця комбінаторика?». Давай розбиратися разом.
Комбінаторика — це розділ математики, який займається вивченням способів упорядкування та комбінування елементів деякої множини відповідно до заданих правил. Це може звучати складно, але насправді ти щодня використовуєш комбінаторику, навіть не усвідомлюючи цього!
Уявімо, що ти вирішив(-ла) одягнути сьогодні улюблені джинси, але ще не придумав(-ла), що вдягти зверху — футболку чи майку. Ти знаєш, що в тебе є  футболок і
футболок і 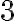 майки. Скількома способами ти зможеш «скласти» своє вбрання на сьогодні? Оскільки ти не будеш одягати футболку і майку одночасно, тобі потрібно вибрати щось одне (футболку АБО майку). Очевидно, що ти можеш вибрати одну з
майки. Скількома способами ти зможеш «скласти» своє вбрання на сьогодні? Оскільки ти не будеш одягати футболку і майку одночасно, тобі потрібно вибрати щось одне (футболку АБО майку). Очевидно, що ти можеш вибрати одну з  футболок або одну із
футболок або одну із 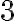 майок, тому разом у тебе
майок, тому разом у тебе 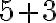 можливих виборів. Цей приклад демонструє одне з базових правил комбінаторики — правило суми.
можливих виборів. Цей приклад демонструє одне з базових правил комбінаторики — правило суми.
Правило суми. Якщо множина A складається з 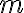 елементів, а множина
елементів, а множина 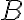 — з
— з 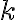 елементів, причому ці множини не мають спільних елементів, то вибір «
елементів, причому ці множини не мають спільних елементів, то вибір «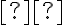 або
або  », де
», де 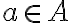 ,
, 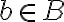 , можна здійснити
, можна здійснити 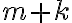 способами.
способами.
Зауважимо, що правило суми можна узагальнити для трьох і більше множин. Наприклад, якщо множини 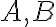 і
і 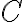 складаються відповідно з
складаються відповідно з 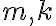 і
і  елементів, причому жодні дві з цих множин не мають спільних елементів, то вибір «
елементів, причому жодні дві з цих множин не мають спільних елементів, то вибір « або
або  або
або 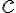 », де
», де 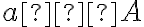 ,
, 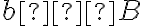 ,
, 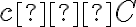 , можна здійснити
, можна здійснити 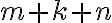 способами.
способами.
Уявімо тепер, що ти хочеш одягнути сьогодні шорти та футболку. Ти знаєш, що у тебе є 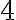 пари шортів і
пари шортів і  футболок. Скількома способами ти зможеш «скласти» своє вбрання на сьогодні? У даному випадку тобі потрібно одночасно одягнути шорти і футболку. Тому, замість правила суми, тобі потрібно застосувати правило добутку і знайти, що у тебе є
футболок. Скількома способами ти зможеш «скласти» своє вбрання на сьогодні? У даному випадку тобі потрібно одночасно одягнути шорти і футболку. Тому, замість правила суми, тобі потрібно застосувати правило добутку і знайти, що у тебе є 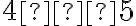 можливих виборів. Тобто, ти маєш
можливих виборів. Тобто, ти маєш 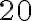 різних варіантів убрання.
різних варіантів убрання.
Правило добутку. Якщо елемент  можна вибрати
можна вибрати 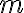 способами, і після кожного такого вибору елемент
способами, і після кожного такого вибору елемент  можна вибрати
можна вибрати 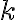 способами, то вибір «
способами, то вибір « і
і  » у вказаному порядку можна здійснити
» у вказаному порядку можна здійснити 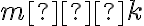 способами.
способами.
Правило добутку, природно, також можна узагальнити. Наприклад, якщо елемент  можна вибрати m способами, після кожного такого вибору елемент
можна вибрати m способами, після кожного такого вибору елемент  можна вибрати
можна вибрати 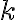 способами, і після того, як вибрано елементи
способами, і після того, як вибрано елементи  і
і  , елемент c можна вибрати
, елемент c можна вибрати  способами, то вибір «
способами, то вибір « і
і  і
і 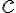 » можна здійснити
» можна здійснити 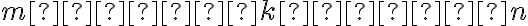 способами.
способами.
Текст розробила Грибель Ольга
з використанням ChatGPT-4.0 та з використанням підручника:
Алгебра: підруч. для 9 кл. загальноосвіт. навч. закладів / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. — Х. : Гімназія, 2017. — 272 с. : іл. ISBN 978-966-474-293-8. URL:https://files.pidruchnyk.com.ua/uploads/book/9_klas_algebra_merzljak_2017.pdf
Картинку до завдання згенерував
Чоп'юк Юрій в ChatGPT 4o.
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour