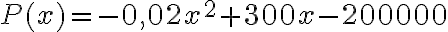Спадання та зростання функції_к
Визначимо основні моменти даного заняття.
1. Зростання та спадання функції. Похідна функції визначає швидкість зміни функції або процесу, який ця функція описує, при зміні аргументу. Якщо похідна додатна, це означає, що функція зростає (швидкість зміни додатна). Якщо похідна від’ємна, це означає, що функція спадає (швидкість зміни від’ємна).
2. Точки екстремуму (максимум та мінімум). Точки екстремуму — це ті точки, в яких функція набуває своїх максимальних або мінімальних значень. Ці точки визначаються як критичні точки, де похідна функції дорівнює нулю або не існує. Якщо знак похідної змінюється з додатного на від’ємний, то точка є максимумом. Якщо знак похідної змінюється з від’ємного на додатний, то точка є мінімумом. Якщо знак похідної не змінюється, то точка не є точкою екстремуму.
3. Абсолютний максимум і мінімум. Абсолютний максимум — це найбільше значення функції на всій її області визначення. Абсолютний мінімум — це найменше значення функції на всій її області визначення. Вони можуть знаходитися в критичних точках або на граничних точках області визначення.

4. Практичне застосування. Застосування похідної відбуваються у багатьох практичних ситуаціях: у фізиці — для визначення швидкості, прискорення, моменту інерції та інших фізичних величин; в економіці — для максимізації прибутку, мінімізації витрат, прийняття оптимальних рішень; в інженерії — для проєктування оптимальних структур і пристроїв; у природничих науках — для вивчення змін у популяціях, екосистемах та інших природних процесах.
Нагадаємо, що функцію 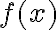 називають зростаючою на інтервалі
називають зростаючою на інтервалі ![[a;~b] [a;~b]](https://lms.smart-osvita.org/filter/tex/pix.php/6eaad4b89290f5aa073f8b9468ef6b30.gif) , якщо більшому значенню
, якщо більшому значенню  відповідає більше значення
відповідає більше значення 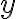 для всіх значень
для всіх значень  із проміжку
із проміжку ![[a;~b] [a;~b]](https://lms.smart-osvita.org/filter/tex/pix.php/6eaad4b89290f5aa073f8b9468ef6b30.gif) . Тобто при
. Тобто при 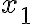
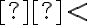
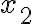 завжди маємо, що
завжди маємо, що 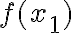
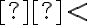
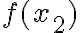 .
.Нагадаємо, що функцію
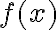 називають спадною на інтервалі
називають спадною на інтервалі ![[a;~b] [a;~b]](https://lms.smart-osvita.org/filter/tex/pix.php/6eaad4b89290f5aa073f8b9468ef6b30.gif) , якщо більшому значенню
, якщо більшому значенню  відповідає менше значення
відповідає менше значення 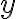 для всіх значень
для всіх значень  із проміжку
із проміжку ![[a;~b] [a;~b]](https://lms.smart-osvita.org/filter/tex/pix.php/6eaad4b89290f5aa073f8b9468ef6b30.gif) . Тобто при
. Тобто при 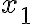
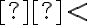
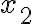 завжди маємо, що
завжди маємо, що 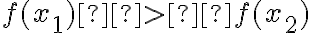 .
.Ці поняття повністю відповідають інтуїтивному «підйому» і «спуску», коли дивимося на графік. Треба пам’ятати про додатний напрямок осі
 , розглядаючи «напрямок» кривої. Тобто ми використовуємо терміни «зростання» та «спадання», щоб описати поведінку функції, коли ми рухаємося зліва направо вздовж її графіка (рис. 1).
, розглядаючи «напрямок» кривої. Тобто ми використовуємо терміни «зростання» та «спадання», щоб описати поведінку функції, коли ми рухаємося зліва направо вздовж її графіка (рис. 1).
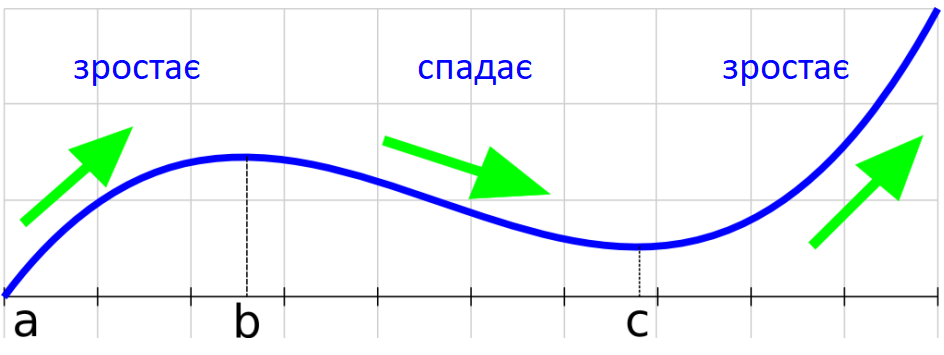
Рисунок 1
Проміжки, на яких функція зростає чи спадає, ще називають проміжками монотонності.На рис. 2 зображено графік зростаючої на проміжку ![[a;~b] [a;~b]](https://lms.smart-osvita.org/filter/tex/pix.php/6eaad4b89290f5aa073f8b9468ef6b30.gif) функції
функції 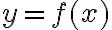 . У якій би точці цього проміжку ми не провели дотичну до графіка функції, кут
. У якій би точці цього проміжку ми не провели дотичну до графіка функції, кут 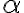 , який вона утворюватиме з додатним напрямом осі абсцис, буде гострий. Оскільки
, який вона утворюватиме з додатним напрямом осі абсцис, буде гострий. Оскільки 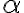 — гострий, то
— гострий, то 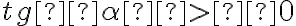 . Тоді, виходячи
з геометричного змісту похідної (
. Тоді, виходячи
з геометричного змісту похідної (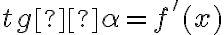 ), можна зробити такий висновок:
для будь-якого
), можна зробити такий висновок:
для будь-якого ![x ∈ [a; b] x ∈ [a; b]](https://lms.smart-osvita.org/filter/tex/pix.php/1b906113d98e5fdf695f36d49cc069f9.gif) виконується нерівність
виконується нерівність 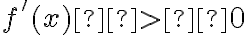 .
.
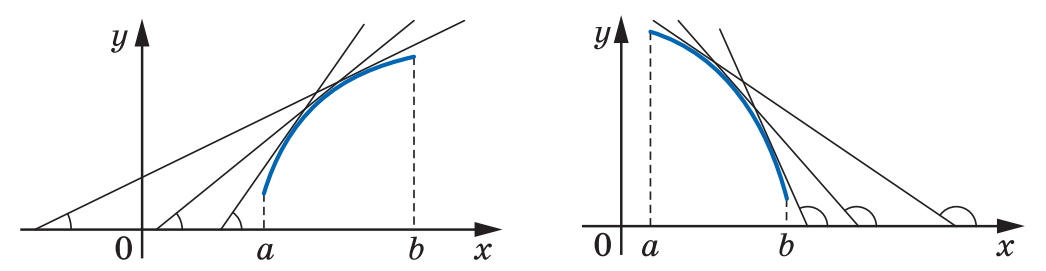
Рисунок 2 Рисунок 3
На рис. 3 зображено графік спадної на проміжку![[a;~b] [a;~b]](https://lms.smart-osvita.org/filter/tex/pix.php/6eaad4b89290f5aa073f8b9468ef6b30.gif) функції
функції 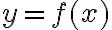 . У кожній точці цього проміжку дотична до графіка функції утворюватиме з додатним напрямом осі
абсцис кут
. У кожній точці цього проміжку дотична до графіка функції утворюватиме з додатним напрямом осі
абсцис кут 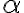 , що є тупим. Оскільки
, що є тупим. Оскільки 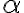 тупий, то
тупий, то 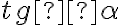
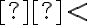
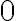 , і
тому
, і
тому 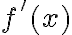
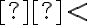
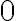 для кожної точки
для кожної точки ![x ∈ [a; b] x ∈ [a; b]](https://lms.smart-osvita.org/filter/tex/pix.php/1b906113d98e5fdf695f36d49cc069f9.gif) .
.
Отже, знаючи, зростає чи спадає функція на певному
проміжку, можна визначити знак похідної на цьому проміжку. А можна і навпаки: за знаком похідної функції на проміжку визначити, зростає ця функція, спадає чи є сталою на
цьому проміжку.
Теорема 1 (ознака сталості функції). Функція
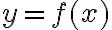 є сталою на проміжку
є сталою на проміжку ![[a;~b] [a;~b]](https://lms.smart-osvita.org/filter/tex/pix.php/6eaad4b89290f5aa073f8b9468ef6b30.gif) тоді й тільки тоді,
коли
тоді й тільки тоді,
коли 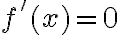 для кожного
для кожного  із цього проміжку.
із цього проміжку.
Теорема 2 (ознака зростання, спадання функції). Якщо
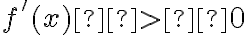 у кожній точці проміжку
у кожній точці проміжку ![[a;~b] [a;~b]](https://lms.smart-osvita.org/filter/tex/pix.php/6eaad4b89290f5aa073f8b9468ef6b30.gif) , то функція
, то функція 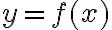 зростає на
зростає на ![[a;~b] [a;~b]](https://lms.smart-osvita.org/filter/tex/pix.php/6eaad4b89290f5aa073f8b9468ef6b30.gif) . Якщо
. Якщо 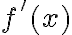
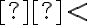
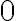 у кожній точці проміжку
у кожній точці проміжку
![[a;~b] [a;~b]](https://lms.smart-osvita.org/filter/tex/pix.php/6eaad4b89290f5aa073f8b9468ef6b30.gif) , то функція
, то функція 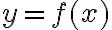 спадає на
спадає на ![[a;~b] [a;~b]](https://lms.smart-osvita.org/filter/tex/pix.php/6eaad4b89290f5aa073f8b9468ef6b30.gif) .
.
Тепер ми можемо визначити знак похідної для функції на рис. 1.
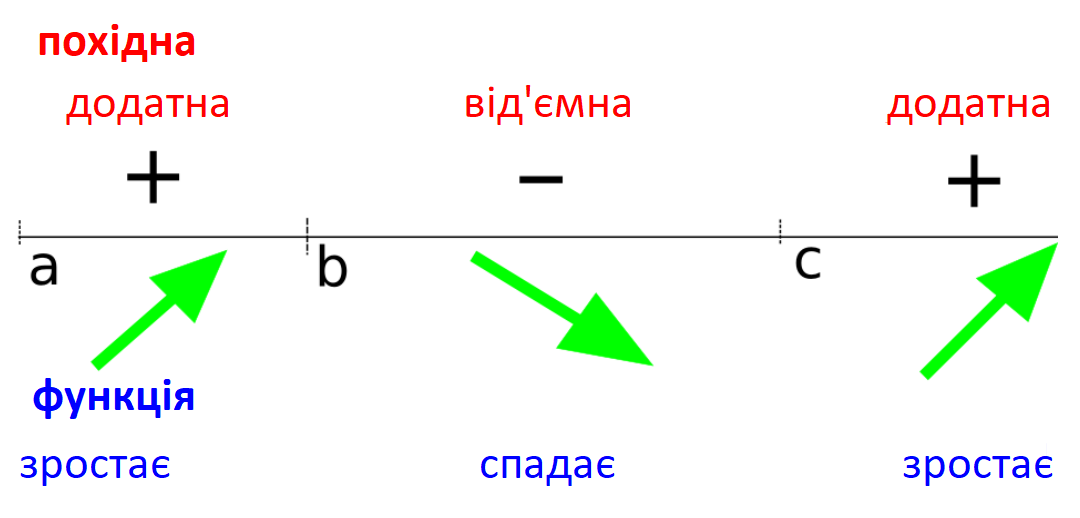
Рисунок 4
Ми бачили, що додатний/від’ємний знак першої похідної точно відповідає зростанню/спаданню функції. Далі ми розглянемо, що відбувається в точках, у яких похідна не є ні додатною, ні від'ємною. У таких точках похідна або дорівнює нулю, або не визначена.На рис. 5 схематично зображено графік функції
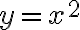 .
.
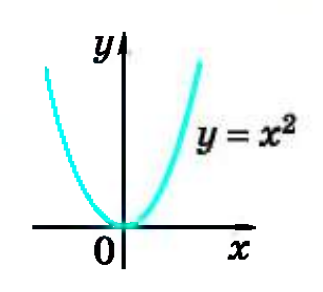
Рисунок 5
Оскільки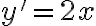 , то
, то 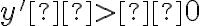 , коли
, коли 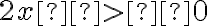 , тобто
при
, тобто
при 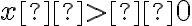 і
і 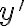
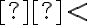
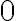 , коли
, коли 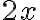
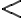
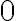 , тобто при
, тобто при 
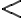
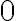 .
Отже, на
.
Отже, на 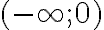 функція спадає, на
функція спадає, на 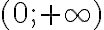 функція зростає, що підтверджується графіком.
У точці
функція зростає, що підтверджується графіком.
У точці 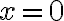 , що розділяє два проміжки, на одному з яких функція спадає, а на іншому — зростає, похідна дорівнює нулю:
, що розділяє два проміжки, на одному з яких функція спадає, а на іншому — зростає, похідна дорівнює нулю: 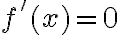 .
.На рис. 6 схематично зображено графік функції
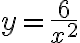 .
.
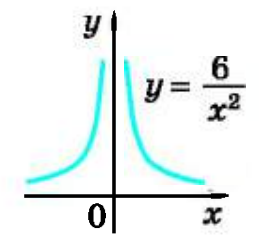
Рисунок 6
Оскільки 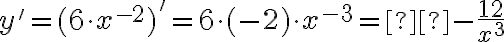 , то
, то 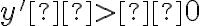 ,
коли
,
коли 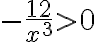 , тобто коли
, тобто коли 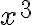
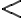
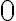 , а значить, при
, а значить, при
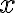
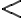
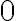 , і
, і 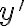
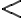
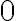 , коли
, коли 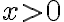 . Отже, на
. Отже, на 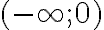 функція зростає, на
функція зростає, на 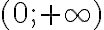 — спадає, що підтверджується графіком. У точці
— спадає, що підтверджується графіком. У точці 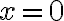 , що розділяє
ці два проміжки, похідна не існує.
Отже, можемо припустити, що два сусідніх
проміжки, на одному з яких функція зростає, а
на іншому — спадає, можуть розділятися точкою, у якій похідна
або не існує, або дорівнює нулю. Якщо така точка належить
області визначення функції, то її називають критичною.
, що розділяє
ці два проміжки, похідна не існує.
Отже, можемо припустити, що два сусідніх
проміжки, на одному з яких функція зростає, а
на іншому — спадає, можуть розділятися точкою, у якій похідна
або не існує, або дорівнює нулю. Якщо така точка належить
області визначення функції, то її називають критичною.
Критичними точками функції називають внутрішні
точки області визначення, для яких похідна функції
не існує або дорівнює нулю.
Для функції 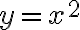 точка
точка 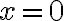 є критичною, а для
є критичною, а для 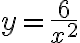 — ні, оскільки не належить області визначення. Отже, точки,
які не належать області визначення, також можуть ділити
графік на проміжки, на одному з яких функція зростає, а на
іншому — спадає.
— ні, оскільки не належить області визначення. Отже, точки,
які не належать області визначення, також можуть ділити
графік на проміжки, на одному з яких функція зростає, а на
іншому — спадає.
Зауважимо, що якщо функція 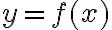 неперервна в точці,
що є кінцем проміжку зростання чи спадання, то цю точку
приєднують до цього проміжку. Таким чином, можна стверджувати, що функція
неперервна в точці,
що є кінцем проміжку зростання чи спадання, то цю точку
приєднують до цього проміжку. Таким чином, можна стверджувати, що функція 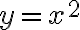 зростає на проміжку
зростає на проміжку 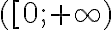 і
спадає на проміжку
і
спадає на проміжку ![(- \infty;~0] (- \infty;~0]](https://lms.smart-osvita.org/filter/tex/pix.php/e786961d2c7a56248de01ca30a343c54.gif) , оскільки в точці
, оскільки в точці 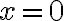 функція
функція 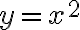 неперервна. Проміжки зростання і спадання функції
неперервна. Проміжки зростання і спадання функції 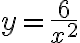 залишаються без змін, оскільки в точці
залишаються без змін, оскільки в точці 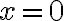 ця функція не є неперервною (має розриви, адже
ця функція не є неперервною (має розриви, адже 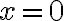 не належить області визначення функції).
не належить області визначення функції).
Зростання і спадання є важливими поняттями, які використовуються не тільки на уроках алгебри, але й у реальному житті та прикладних науках. Вони допомагають аналізувати зміни і динаміку функцій та процесів у різних контекстах.
Зростання функції означає збільшення значень функції зі збільшенням аргументу (наприклад, часу, відстані, об'єму тощо). У реальному житті це може бути приріст кількості населення, збільшення швидкості руху певного транспортного засобу або зростання обсягів продажів товарів. Спадання функції означає зменшення значень функції зі збільшенням аргументу. У реальному житті це може бути скорочення кількості населення, зменшення швидкості руху певного транспортного засобу або спад обсягів продажів товарів.
Прикладна задача. Функція прибутку.
Функція прибутку компанії Acrosonic визначається як
доларів, де  — кількість вироблених акустичних систем Acrosonic моделі F. Знайти, де функція
— кількість вироблених акустичних систем Acrosonic моделі F. Знайти, де функція 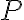 зростає, а де — спадає.
зростає, а де — спадає.
Розв’язання. 1. Знайдемо область визначення функції. 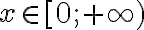 , оскільки
, оскільки  — це кількість.
— це кількість.
2. Знайдемо похідну 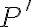 функції
функції 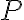 :
: 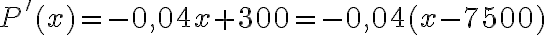 .
.
3. Знайдемо критичні точки функції: 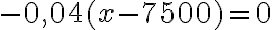 . Таким чином,
. Таким чином, 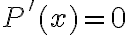 , коли
, коли 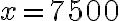 .
.
4. Поділимо знайденою критичною точкою область визначення функції на проміжки. Отримаємо: ![[0;~ 7500] \cup [7500;~+ \infty) [0;~ 7500] \cup [7500;~+ \infty)](https://lms.smart-osvita.org/filter/tex/pix.php/0ba138bb6b12073c740b33e65d9d7a43.gif) .
.
5. З'ясуємо знак похідної на вказаних проміжках. Підставимо точку з першого проміжка в рівняння похідної. Наприклад, 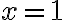 , будемо мати
, будемо мати 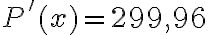 . Підставимо точку з другого проміжка в рівняння похідної. Наприклад,
. Підставимо точку з другого проміжка в рівняння похідної. Наприклад, 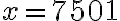 , будемо мати
, будемо мати 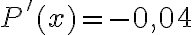 . Отже,
. Отже, 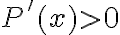 для
для  в інтервалі
в інтервалі ![[0;~ 7500] [0;~ 7500]](https://lms.smart-osvita.org/filter/tex/pix.php/1a9da08c8515ae4f28ee30ca17f092d5.gif) , а
, а 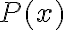
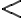
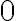 для
для  в інтервалі
в інтервалі 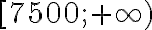 .
.
6. Це означає, що функція прибутку 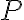 зростає на
зростає на ![[0;~ 7500] [0;~ 7500]](https://lms.smart-osvita.org/filter/tex/pix.php/1a9da08c8515ae4f28ee30ca17f092d5.gif) і спадає на
і спадає на 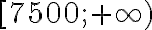 .
.
Теорію впорядкувала Луців Ілона-Анна.
Джерела:
- Алгебра 10 клас. Мерзляк А. Г.,Номіровський Д. А., Полонський В. Б., Якір М. С.
- Алгебра 10 клас. Істер О., Єргіна О.
- Applied Mathematics: For the Managerial, Life, and Social Sciences (5th Edition). Tan S.T.
- Calculus 1. Increasing/Decreasing Test. Extreme Values and The First Derivative Test. Lia Vas
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour