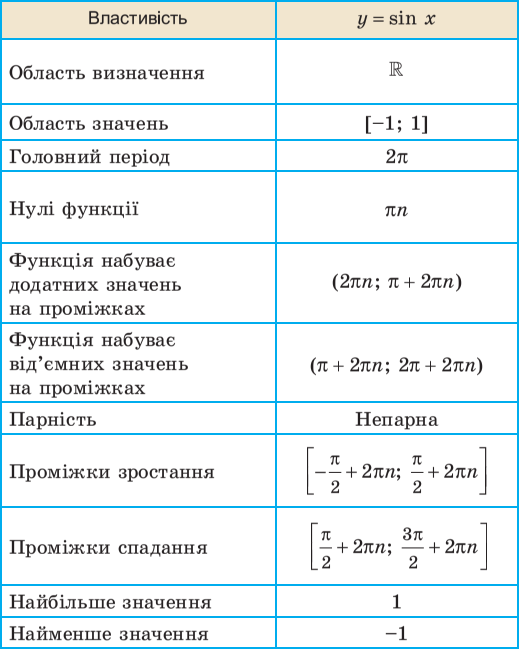
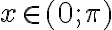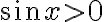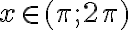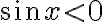Графік і властивості функції y = sin x
Розглянемо функцію 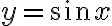 на проміжку
на проміжку ![[0; 2 \pi] [0; 2 \pi]](https://lms.smart-osvita.org/filter/tex/pix.php/d0034cb1fddc04d18d3481be97eab228.gif) , тобто на проміжку завдовжки в період цієї функції.
, тобто на проміжку завдовжки в період цієї функції.
Під час повороту точки 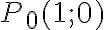 навколо початку координат на кути від
навколо початку координат на кути від 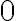 до
до 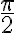 більшому куту повороту відповідає точка одиничного кола з більшою ординатою. Це означає, що функція
більшому куту повороту відповідає точка одиничного кола з більшою ординатою. Це означає, що функція 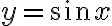 зростає на проміжку
зростає на проміжку ![\left[0 ; \frac{\pi}{2}\right] \left[0 ; \frac{\pi}{2}\right]](https://lms.smart-osvita.org/filter/tex/pix.php/fa77e804d957bb1ba840afd1ff3cf570.gif) .
.
Під час повороту точки 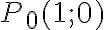 на кути від
на кути від 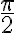 до
до 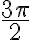 більшому куту повороту відповідає точка одиничного кола з меншою ординатою. Отже, функція
більшому куту повороту відповідає точка одиничного кола з меншою ординатою. Отже, функція 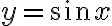 спадає на проміжку
спадає на проміжку ![\left[\frac{\pi}{2} ; \frac{3 \pi}{2}\right] \left[\frac{\pi}{2} ; \frac{3 \pi}{2}\right]](https://lms.smart-osvita.org/filter/tex/pix.php/dbdc4973cf635f1e86a74ab57e6a4689.gif) .
.
Під час повороту точки 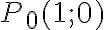 на кути від
на кути від 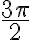 до
до 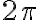 більшому куту повороту відповідає точка одиничного кола з більшою ординатою. Отже, функція
більшому куту повороту відповідає точка одиничного кола з більшою ординатою. Отже, функція 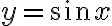 зростає на проміжку
зростає на проміжку ![\left[\frac{3 \pi}{2} ; 2 \pi\right] \left[\frac{3 \pi}{2} ; 2 \pi\right]](https://lms.smart-osvita.org/filter/tex/pix.php/2946a120b9dcac11276f9f2d1e705c43.gif) .
.
Функція 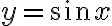 на проміжку
на проміжку ![[0; 2 \pi] [0; 2 \pi]](https://lms.smart-osvita.org/filter/tex/pix.php/d0034cb1fddc04d18d3481be97eab228.gif) досягає найбільшого значення, яке дорівнює
досягає найбільшого значення, яке дорівнює 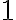 , при
, при 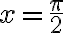 , і найменшого значення, яке дорівнює
, і найменшого значення, яке дорівнює 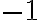 , при
, при 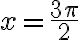 .
.
Функція 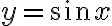 на проміжку
на проміжку ![[0 ; 2 \pi] [0 ; 2 \pi]](https://lms.smart-osvita.org/filter/tex/pix.php/0b242c079d0219dced553a339f6e1457.gif) набуває всіх значень із проміжку
набуває всіх значень із проміжку ![[-1 ; 1] [-1 ; 1]](https://lms.smart-osvita.org/filter/tex/pix.php/1aa123cd663ae984bfc6216ef551deae.gif) .
.
Отримані властивості функції 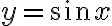 дають змогу побудувати їі графік на проміжку
дають змогу побудувати їі графік на проміжку ![[0 ; 2 \pi] [0 ; 2 \pi]](https://lms.smart-osvita.org/filter/tex/pix.php/0b242c079d0219dced553a339f6e1457.gif) .
.

На всій області визначення графік функції 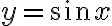 можна отримати з побудованого графіка за допомогою паралельних перенесень на вектори з координатами
можна отримати з побудованого графіка за допомогою паралельних перенесень на вектори з координатами 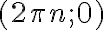 ,
, 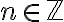 .
.
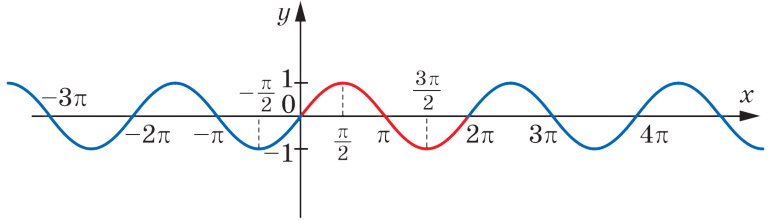
Графік функції 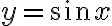 називають синусоїдою.
називають синусоїдою.
Нижче у таблиці наведено основні властивості функцій 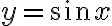 .
.
Джерело: Математика : алгебра і початки аналізу та геометрія, рівень стандарту : підруч. для 10 кл. закладів загальної середньої освіти / А. Г. Мерзляк, Д. А. Номіровський, В. Б. Полонський, М. С. Якір. — Х. : Гімназія, 2018. —256 с. : іл. ISBN 978-966-474-310-2. URL:https://pidruchnyk.com.ua/1153-matematyka-10-klas-merzlyak.html
Джерело зображення: https://formula.kr.ua/trigonometriya/oznachennya-ta-vlastivosti-trigonometrichnih-funktsiy/
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour