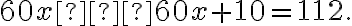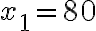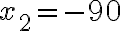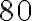Вчимося складати квадратне рівняння за задачею
Складання математичних моделей задач — це процес перетворення реальних ситуацій на математичні вирази, які допомагають краще зрозуміти цю ситуацію і знайти розв’язок. Наприклад, нам потрібно розрахувати, скільки грошей ми можемо заробити за певний час. Для цього ми можемо скласти формулу, де кількість грошей залежить від часу і швидкості заробітку, і спрогнозувати, скільки грошей можна заробити, якщо змінювати час чи швидкість роботи.
Математичні моделі задач дозволяють краще розуміти складні ситуації і дають можливість приймати правильні рішення. Такі моlелі тобі вже зустрічалися раніше! Ознайомся з поданими нижче прикладами і алгоритмом застосування математичних моделей для раціональних рівнянь.
 ПРИКЛАД 1. Перегін у
ПРИКЛАД 1. Перегін у 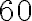 км поїзд мав проїхати з постійною швидкістю за визначений розкладом час. Поїзд простояв перед перегоном
км поїзд мав проїхати з постійною швидкістю за визначений розкладом час. Поїзд простояв перед перегоном  хв, тому машиніст був змушений збільшити швидкість на перегоні на
хв, тому машиніст був змушений збільшити швидкість на перегоні на 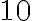 км/год, щоб надолужити втрачені
км/год, щоб надолужити втрачені  хв.
хв.
З якою швидкістю поїзд повинен був пройти перегін за розкладом?
Перший етап. Складання математичної моделі.
Нехай  км/год — швидкість поїзда за розкладом.
км/год — швидкість поїзда за розкладом.
Оскільки протяжність перегону дорівнює 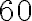 км, то час, відведений розкладом на проходження перегону, становить
км, то час, відведений розкладом на проходження перегону, становить 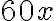 год.
год.
Фактично поїзд пройшов перегін протяжністю 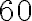 км зі швидкістю
км зі швидкістю 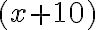 км/год. Отже, час, витрачений на проходження перегону, дорівнює
км/год. Отже, час, витрачений на проходження перегону, дорівнює 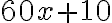 год.
год.
Із двох величин — 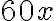 год і
год і 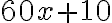 год перша більше від другої на
год перша більше від другої на  хв, тобто на
хв, тобто на 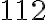 год.
год.
Математична модель задачі складена. Це раціональне рівняння.
Другий етап. Робота зі складеною моделлю.
Маємо:
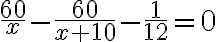 .
Перетворимо ліву частину рівняння:
.
Перетворимо ліву частину рівняння:
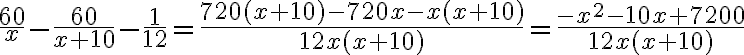 .
.
Прирівнявши чисельник цього дробу до нуля, отримаємо квадратне рівняння 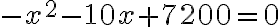 або, переходячи до більш зручного запису,
або, переходячи до більш зручного запису, 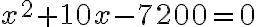 .
.
Далі розв’яжемо квадратне рівняння за допомогою дискримінанта, як на попередньому уроці.
Обидва значення задовольняють умову 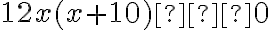 . Отже, ці значення — корені складеного раціонального рівняння.
. Отже, ці значення — корені складеного раціонального рівняння.
Третій етап. Відповідь на питання задачі.
У задачі запитують: з якою швидкістю поїзд повинен був пройти перегін за розкладом?
Саме цю величину ми позначили буквою 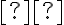 і отримали два значення:
і отримали два значення: 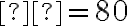 або
або 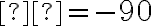 . Друге значення нас не влаштовує, оскільки швидкість руху поїзда не може виражатися від'ємним числом. Отже, вибираємо значення
. Друге значення нас не влаштовує, оскільки швидкість руху поїзда не може виражатися від'ємним числом. Отже, вибираємо значення 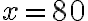 — це і є відповідь на питання задачі.
— це і є відповідь на питання задачі.
 км/год — швидкість поїзда за розкладом.
км/год — швидкість поїзда за розкладом.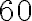 км, то час, відведений розкладом на проходження перегону, становить
км, то час, відведений розкладом на проходження перегону, становить 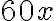 год.
год.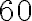 км зі швидкістю
км зі швидкістю 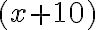 км/год. Отже, час, витрачений на проходження перегону, дорівнює
км/год. Отже, час, витрачений на проходження перегону, дорівнює 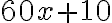 год.
год.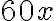 год і
год і 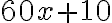 год перша більше від другої на
год перша більше від другої на  хв, тобто на
хв, тобто на 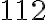 год.
год.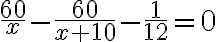 .
Перетворимо ліву частину рівняння:
.
Перетворимо ліву частину рівняння:
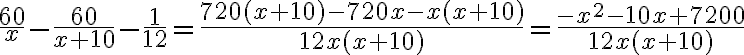 .
.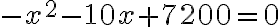 або, переходячи до більш зручного запису,
або, переходячи до більш зручного запису, 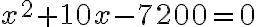 .
.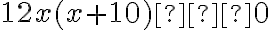 . Отже, ці значення — корені складеного раціонального рівняння.
. Отже, ці значення — корені складеного раціонального рівняння.
ПРИКЛАД 2. Одна бригада працювала на ремонті дороги 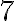 год, після чого до неї приєдналася друга бригада. Через
год, після чого до неї приєдналася друга бригада. Через  год їхньої спільної роботи ремонт було закінчено.
год їхньої спільної роботи ремонт було закінчено.
За скільки годин може відремонтувати дорогу кожна бригада, працюючи самостійно, якщо першій для цього потрібно на 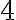 год більше, ніж другій?
год більше, ніж другій?
Розв’язання. Нехай перша бригада може самостійно відремонтувати дорогу за  год, тоді другій для цього потрібно
год, тоді другій для цього потрібно 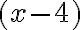 год. За 1 год перша бригада ремонтує
год. За 1 год перша бригада ремонтує 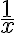 частину дороги, а друга
частину дороги, а друга 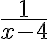 частину дороги. Перша бригада працювала 9 год і відремонтувала
частину дороги. Перша бригада працювала 9 год і відремонтувала 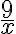 дороги, а друга бригада працювала 2 год і відремонтувала відповідно
дороги, а друга бригада працювала 2 год і відремонтувала відповідно 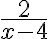 дороги. Оскільки в результаті було відремонтовано всю дорогу, то можна скласти рівняння
дороги. Оскільки в результаті було відремонтовано всю дорогу, то можна скласти рівняння 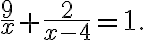
Отримане рівняння має два корені: 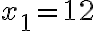 і
і 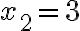 (переконайся в цьому самостійно). Другий корінь не задовольняє умову задачі, оскільки тоді друга бригада мала б відремонтувати дорогу за
(переконайся в цьому самостійно). Другий корінь не задовольняє умову задачі, оскільки тоді друга бригада мала б відремонтувати дорогу за 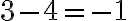 (год), що не має змісту.
(год), що не має змісту.
Отже, перша бригада може відремонтувати дорогу за 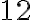 год, а друга — за
год, а друга — за 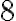 год.
год.
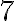 год, після чого до неї приєдналася друга бригада. Через
год, після чого до неї приєдналася друга бригада. Через  год їхньої спільної роботи ремонт було закінчено.
год їхньої спільної роботи ремонт було закінчено. 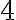 год більше, ніж другій?
год більше, ніж другій? год, тоді другій для цього потрібно
год, тоді другій для цього потрібно 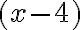 год. За 1 год перша бригада ремонтує
год. За 1 год перша бригада ремонтує 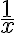 частину дороги, а друга
частину дороги, а друга 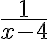 частину дороги. Перша бригада працювала 9 год і відремонтувала
частину дороги. Перша бригада працювала 9 год і відремонтувала 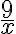 дороги, а друга бригада працювала 2 год і відремонтувала відповідно
дороги, а друга бригада працювала 2 год і відремонтувала відповідно 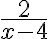 дороги. Оскільки в результаті було відремонтовано всю дорогу, то можна скласти рівняння
дороги. Оскільки в результаті було відремонтовано всю дорогу, то можна скласти рівняння 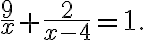
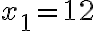 і
і 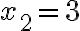 (переконайся в цьому самостійно). Другий корінь не задовольняє умову задачі, оскільки тоді друга бригада мала б відремонтувати дорогу за
(переконайся в цьому самостійно). Другий корінь не задовольняє умову задачі, оскільки тоді друга бригада мала б відремонтувати дорогу за 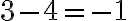 (год), що не має змісту.
(год), що не має змісту.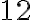 год, а друга — за
год, а друга — за 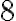 год.
год. Теорію
розробила Радул Андріана з використання платформи "Мій клас" та підручником вказаним нижче.
Картинку до прикладів згенерувала
Грибель Ольга в ChatGPT-4.0.Джерело: А.Г. Мерзляк, В.Б. Полонський, М.С. Якір. Алгебра: підручник для 8-го класу. 2021 рік. Шкільні підручники онлайн. URL: https://files.pidruchnyk.com.ua/uploads/book/8-klas-alhebra-merzlyak-2021.pdf
"Мій клас"
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour