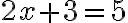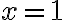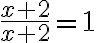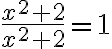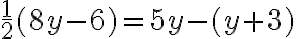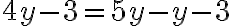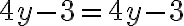Математика jul_2024_8_8: Розв’язуємо рівняння | Smartosvita LMS

Розв’язуємо рівняння

Досить часто в шкільних підручниках ти зустрічаєш слова «рівняння» і «тотожність». Давай з’ясуємо, чим же вони відрізняються.

Вікіпедія дає нам таке формулювання: «Тотожність — рівність двох виразів, яка виконується на всій множині значень змінних (рівність, що виконується для будь-яких значень змінної). Рівність 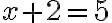$x+2=5$ має місце не для будь-якого значення, а тільки при 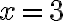$x=3$ . Така рівність не є тотожністю — вона називається рівнянням».

Тепер спробуємо розібратися із цим детальніше та перекласти на «людську мову» ;)

Рівняння буде правильним лише при певному конкретному значенні $x$ . Тут важливо зауважити, що таке значення може бути і не одне — їх може бути як скінченна, так і нескінченна кількість, проте не для всіх можливих чисел.

Неформально, тотожністю буде рівняння, що завжди правильне, тобто буде правильне для кожного без винятку значення $x$ . Якщо рівняння не виконується навіть для однісінького числа, називати його тотожністю ми вже не зможемо.

Розглянемо деякі приклади, щоб краще зрозуміти відмінності.

$2x+3=5$ ;

$x=1$

Як бачимо, тут лише один розв’язок. Висновок: перед нами рівняння.

$\frac{x+2}{x+2}=1$

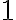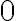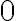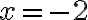Тут ти і попавсь) Не все, що має вигляд тотожності, насправді нею є! Звісно, число, поділене саме на себе, буде дорівнювати $1$ . Винятком буде лише випадок, коли це число дорівнює $0$ . Знаменник нашого дробу перетворюється в $0$ при $x=-2$ .Отже, існує таке число (у нашому прикладі це 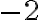$-2$ ), при якому вираз стає неправильним, бо на нуль ділити не можна. Отже, перед нами також рівняння.

$\frac{x^2+2}{x^2+2}=1$

У цьому випадку проблеми зі знаменником немає, і дріб справді буде дорівнювати 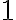$1$ для всіх дійсних значеннь $x$ .

$\frac{1}{2}(8 y-6)=5 y-(y+3)$ $4 y-3=5 y-y-3$

$4 y-3=4 y-3$

Рівність справедлива для всіх значень 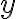$y$ . Це рівняння є тотожністю.

Довести тотожність означає встановити, що за всіх допустимих значень змінних його ліва і права частини є тотожно рівними виразами.

Тотожності можна доводити різними способами:

Виконати перетворення лівої частини та звести до правої частини.

Виконати перетворення правої частини та звести до лівої частини.

Окремо виконати праву та ліву частини й отримати той самий вираз у першому та другому випадках.

Скласти різницю лівої та правої частин, отримавши в результаті нуль.

Тепер розглянемо приклад.

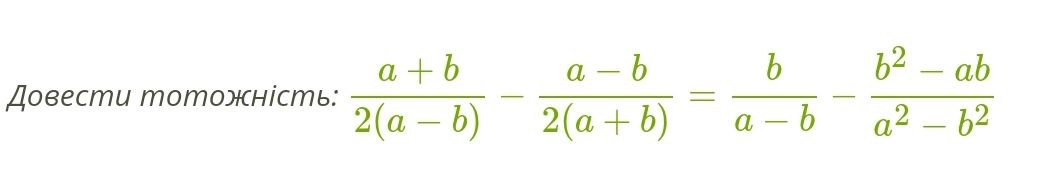
Розв’язання.

_{Теорію розробила Радул Андріана.}

Джерело: Вікіпедія та платформа "Мій клас".

Метод оцінювання: Краща оцінка.