Зв’язок між коренем і квадратом
Поняття квадратного кореня
Пригадай: квадратний корінь числа — це таке число
— це таке число  , яке при множенні на себе (тобто в квадраті) дає вихідне число
, яке при множенні на себе (тобто в квадраті) дає вихідне число  .
.Наприклад,
 — це квадратний корінь з
— це квадратний корінь з 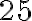 , тому що
, тому що 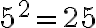 . Оскільки
. Оскільки 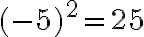 , то
, то 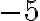 — це теж квадратний корінь з
— це теж квадратний корінь з 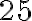 .
. Отже, кожне додатне дійсне число має два квадратні корені (додатний та від’ємний). З цієї причини ми використовуємо знак радикала 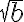 для позначення арифметичного (невід’ємного) квадратного кореня і
для позначення арифметичного (невід’ємного) квадратного кореня і 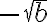 для позначення від’ємного квадратного кореня.
для позначення від’ємного квадратного кореня.
Якщо ми розглянемо рівняння 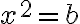 , то воно має два розв’язки: додатний і від’ємний.
, то воно має два розв’язки: додатний і від’ємний.
Приклад. 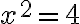 має розв’язки:
має розв’язки: 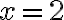 і
і 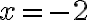 .
При цьому
.
При цьому  і
і 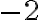 — це квадратні корені з числа
— це квадратні корені з числа 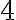 ,
число
,
число  — арифметичний квадратний корінь з числа
— арифметичний квадратний корінь з числа 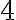 .
.
Теорію розробила Расяк Юлія.
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour