Множення раціональних чисел
Ситуація. Бабуся попросила онука допомогти порахувати, скільки літрів соку вміститься у п’ять дволітрових банок. Петрик пригадав, що додавання кількох рівних додатних чисел можна замінити дією множення. Тоді: 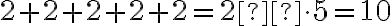 .
.
Чи правильно міркував Петрик? Так. Він міркував правильно й отримав, що  банок по
банок по  л міститимуть
л міститимуть 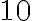 л соку.
л соку.
Кожне раціональне число характеризують його модуль і знак, тому модуль і знак характеризують і добуток чисел.
Дані про модуль і знак додатних чисел та їх добутку наведено в таблиці.

Множення від’ємного і додатного чисел
Як від’ємне число помножити на додатне число? Поміркуємо аналогічно до попереднього прикладу.
Знайдемо добуток чисел 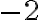 і
і  :
:
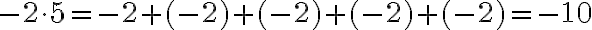 . Отримане число
. Отримане число 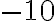 є протилежним до числа
є протилежним до числа 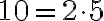 . Але
. Але 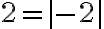 ,
, 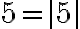 . Отже, добуток чисел
. Отже, добуток чисел 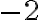 і
і  дорівнює добутку модулів цих чисел, узятому зі знаком
дорівнює добутку модулів цих чисел, узятому зі знаком 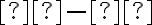 :
: 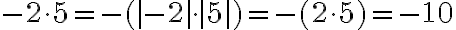 .
.
Як помножити числа  і
і 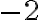 ? Поміркуємо, спираючись на термометр.
? Поміркуємо, спираючись на термометр.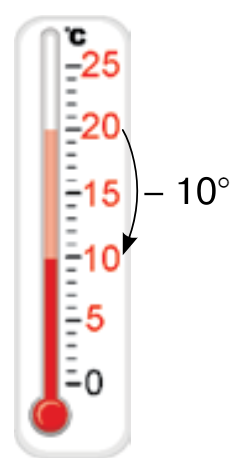 Нехай, наприклад,
Нехай, наприклад, 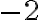 — це зміна температури повітря щогодини, а
— це зміна температури повітря щогодини, а  — кількість годин, протягом яких велося спостереження. Тоді і добуток
— кількість годин, протягом яких велося спостереження. Тоді і добуток
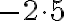 , і добуток
, і добуток 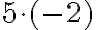 показує, на скільки градусів змінилася температура за 5 год і в який саме бік — підвищення чи зниження. Зрозуміло, що похолодало на
показує, на скільки градусів змінилася температура за 5 год і в який саме бік — підвищення чи зниження. Зрозуміло, що похолодало на 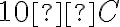 , тобто температура змінилась на
, тобто температура змінилась на 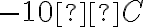 .
.
Одержали, що 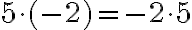 . Тому
. Тому 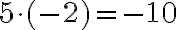 . Отже, добуток чисел
. Отже, добуток чисел  і
і 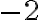 можна знайти так само, як і добуток чисел
можна знайти так само, як і добуток чисел 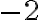 і
і  :
:
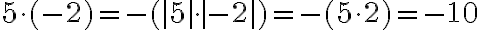 .
.
Занесемо дані в таблиці та з’ясуємо, як знаходили модуль і знак добутку в обох випадках.
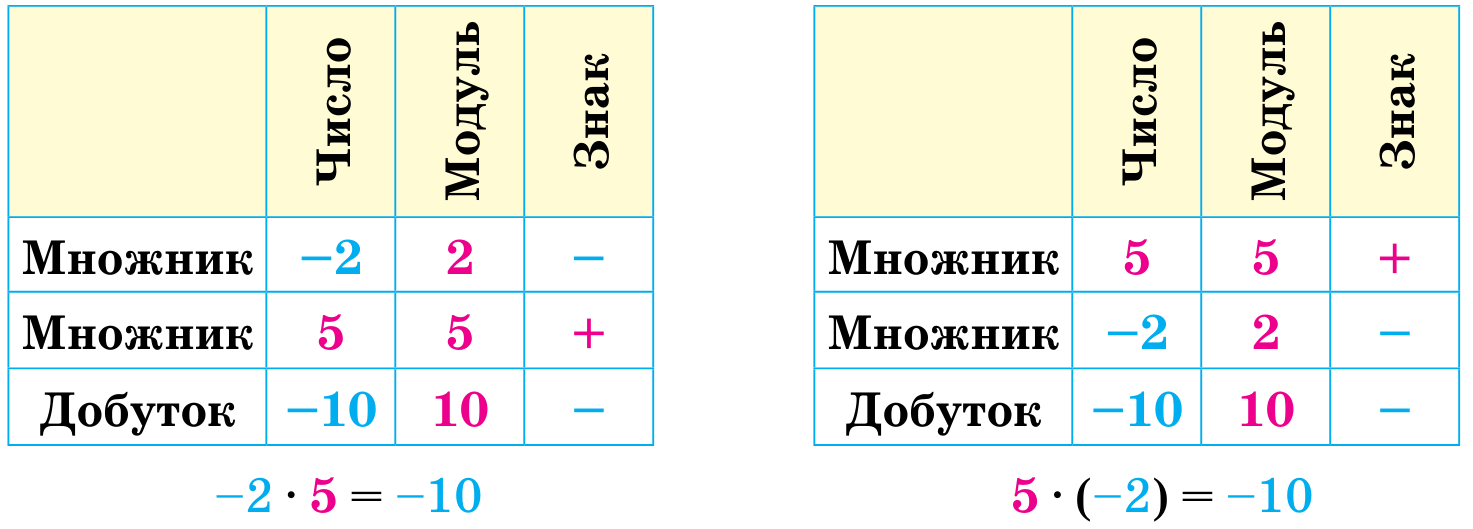
Добуток двох чисел з різними знаками — число
від’ємне.
Щоб помножити два числа з різними знаками, треба
помножити їх модулі й перед отриманим добутком поставити знак «-».
Чи зміниться добуток чисел з різними знаками, якщо їх
множити в іншому порядку? Ні, добуток не зміниться.
Множення двох від’ємних чисел
Як помножити два від’ємні числа? Поміркуємо.
Задача. Температура повітря щогодини
змінювалась на 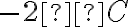 . Якою була температура
. Якою була температура  год тому?
год тому?
Розв’язання. Якщо число  — це кількість
годин, протягом яких велися спостереження, то число
— це кількість
годин, протягом яких велися спостереження, то число 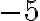 відповідає часу «5
год тому». Отже, у задачі треба знайти добуток
відповідає часу «5
год тому». Отже, у задачі треба знайти добуток 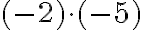 .
Зрозуміло, що
.
Зрозуміло, що  год тому було тепліше на
год тому було тепліше на 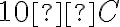 . Тобто
. Тобто
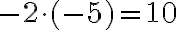 . Отже,
добуток двох від’ємних чисел є числом додатним, яке дорівнює добутку модулів
множників. Наприклад:
. Отже,
добуток двох від’ємних чисел є числом додатним, яке дорівнює добутку модулів
множників. Наприклад:
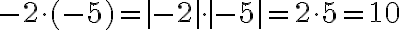 .
.
Дані про модуль і знак чисел та їх добутку
наведено в таблиці.

Якщо добуток двох раціональних чисел додатний, то множники є числами з однаковими знаками. Якщо добуток двох раціональних чисел від’ємний, то множники є числами з різними знаками.
Знак добутку кількох раціональних чисел
Чи можна визначити знак добутку кількох раціональних чисел, не обчислюючи цей добуток?
Так. При цьому враховують, що добуток додатних множників є додатним, і вони не впливають на знак результату.
Добуток парної кількості від’ємних множників — додатний.
Добуток непарної кількості від’ємних множників — від’ємний.
Деякі властивості множення раціональних чисел
- Якщо один із множників дорівнює нулю, то добуток дорівнює нулю:
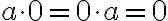 .
. - Якщо один із множників дорівнює
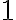 , то добуток дорівнює іншому множнику:
, то добуток дорівнює іншому множнику:
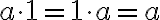 .
. - Якщо деяке число помножити на
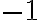 , то в добутку одержимо протилежне до
нього число:
, то в добутку одержимо протилежне до
нього число: 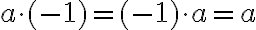 .
.
Чи справджуються для раціональних чисел переставний і сполучний закони множення, а також розподільний закон множення відносно додавання? Так.
Для будь-яких раціональних чисел 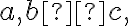 відмінних від нуля:
відмінних від нуля:
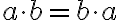 — переставний закон множення;
— переставний закон множення; 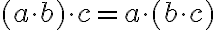 — сполучний закон множення;
— сполучний закон множення; 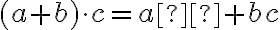 —
розподільний закон множення відносно додавання.
—
розподільний закон множення відносно додавання.
Джерело: Н.А. Тарасенкова, І.М. Богатирьова, О.М. Коломієць, З.О. Сердюк, Ю.В. Рудніцька. Математика: підручник для 6-го класу. Частина 2. 2023 рік. Шкільні підручники онлайн. https://pidruchnyk.com.ua/2588-matematyka-6-klas-tarasenkova-2023.html
Картинку до теорії згенерував Чоп'юк Юрій в ChatGPT-4o.
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour
