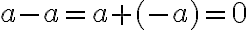Віднімання раціональних чисел
Чи правильно Юрко показав на координатній прямій, як від числа 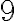 відняти число
відняти число 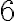 ?
?

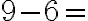
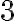 .
.Дія віднімання для раціональних чисел має той самий зміст, що й для натуральних: віднімаючи від числа  число
число  , ми шукаємо таке число, яке в сумі з числом
, ми шукаємо таке число, яке в сумі з числом  дає число
дає число  .
.
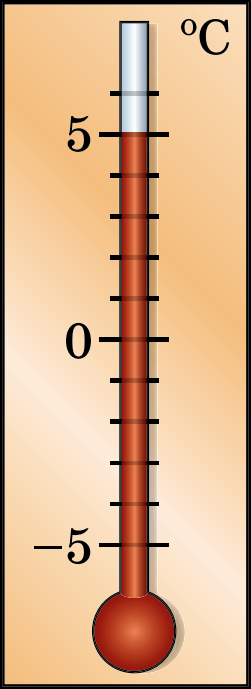
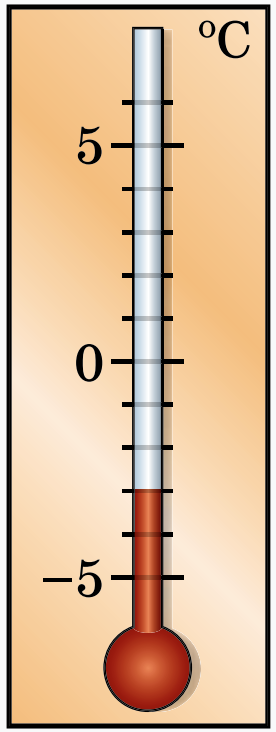 Нехай опівдні температура повітря дорівнювала
Нехай опівдні температура повітря дорівнювала 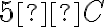 , а до вечора вона зменшилася на
, а до вечора вона зменшилася на 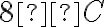 . Тоді температура повітря ввечері дорівнювала
. Тоді температура повітря ввечері дорівнювала 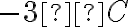 .
.
Тому різницею чисел  і
і 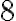 є число
є число 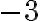 :
:
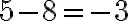 .
Як перевірити, чи віднімання виконано правильно?
Додамо до різниці
.
Як перевірити, чи віднімання виконано правильно?
Додамо до різниці 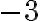 від’ємник
від’ємник 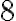 :
:
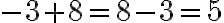 — одержали зменшуване. Отже, віднімання виконано правильно.
— одержали зменшуване. Отже, віднімання виконано правильно.
Зауважимо, що раніше ми не могли від меншого числа відняти більше. Завдяки від’ємним числам таке віднімання стало можливим: якщо від числа  віднімемо число
віднімемо число 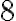 , то одержимо від’ємне число
, то одержимо від’ємне число 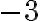 . Такий самий результат одержимо, якщо до числа
. Такий самий результат одержимо, якщо до числа  додамо число, протилежне числу
додамо число, протилежне числу 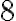 :
:
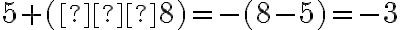 . Маємо правильну рівність:
. Маємо правильну рівність: 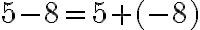 .
.
Отже, дію віднімання можна замінити дією додавання: щоб від числа  відняти
відняти 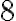 , досить до зменшуваного (числа
, досить до зменшуваного (числа  ) додати число, протилежне від’ємнику (числу
) додати число, протилежне від’ємнику (числу 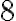 ).
).
Узагалі, для будь-яких раціональних чисел виконується таке правило віднімання:
Щоб знайти різницю двох чисел, досить до зменшуваного додати число, протилежне від’ємнику.
Це правило можна записати так:
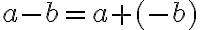 , де
, де  і
і  — будь-які раціональні числа.
— будь-які раціональні числа.
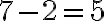 ,
, 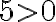 ;
;
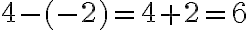 ,
, 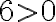 .
.
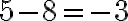 ,
, 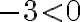 ;
;
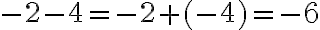 ,
, 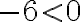 .
.
Оскільки дію віднімання можна замінити операцією додавання протилежного числа, будь-який вираз, який містить дії додавання і віднімання, можна записати у вигляді суми. Наприклад,
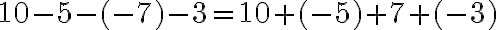 .
.
Джерела:
- Н.А. Тарасенкова, І.М. Богатирьова, О.М. Коломієць, З.О. Сердюк, Ю.В. Рудніцька. Математика: підручник для 6-го класу. Частина 2. 2023 рік. Шкільні підручники онлайн.
https://pidruchnyk.com.ua/2588-matematyka-6-klas-tarasenkova-2023.html
- В.Р. Кравчук, Г.М. Янченко. Математика: підручник для 6-го класу. 2023 рік. Шкільні підручники онлайн.
https://pidruchnyk.com.ua/2586-matematyka-6-klas-kravchuk-2023.html ;
- О.С. Істер. Математика: підручник для 6-го класу. Частина 2. 2023 рік. Шкільні підручники онлайн.
URL: https://pidruchnyk.com.ua/2590-matematyka-6-klas-ister-2023.html
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour