Розв’язання ірраціональних рівнянь за допомогою ОДЗ
Ірраціональними називаються рівняння, в яких невідома величина знаходиться під знаком кореня (радикала) або під знаком дії піднесення до дробового показника степеня.
Основним методом розв’язування ірраціональних рівнянь є перетворення їх на раціональні рівняння.
При розв’язуванні ірраціональних рівнянь використовуються теореми:
Теорема 1. Рівняння вигляду ![\sqrt[2 n]{f(x)}=a \sqrt[2 n]{f(x)}=a](https://lms.smart-osvita.org/filter/tex/pix.php/a56a359ccbc21da3d4d8016410f77796.gif) рівносильне сукупності систем
рівносильне сукупності систем
Теорема 2. Рівняння вигляду 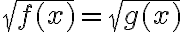 рівносильне системі
рівносильне системі
3 двох систем вибирається та, яка простіше розв’язується.
Теорема 3. Рівняння вигляду ![\sqrt[2 n]{f(x)}=g(x) \sqrt[2 n]{f(x)}=g(x)](https://lms.smart-osvita.org/filter/tex/pix.php/adfd8af6463c2ddcdad3f439c511f959.gif) рівносильне системі
рівносильне системі 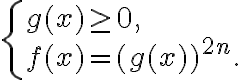
Теорема 4. Рівняння вигляду ![\sqrt[2 n+1]{f(x)}=g(x) \sqrt[2 n+1]{f(x)}=g(x)](https://lms.smart-osvita.org/filter/tex/pix.php/f81c58642cc392572a433d74d76eb61e.gif) рівносильне рівнянню
рівносильне рівнянню 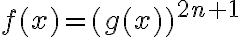 .
.
Теорема 5. Рівняння вигляду ![\sqrt[2 n]{f(x)} \cdot g(x)=0 \sqrt[2 n]{f(x)} \cdot g(x)=0](https://lms.smart-osvita.org/filter/tex/pix.php/f57f3b7754e203613a636ecc729e1afb.gif) рівносильне сукупності систем
рівносильне сукупності систем 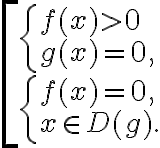
Теорема 6. Рівняння вигляду ![\frac{\sqrt[2 n]{f(x)}}{g(x)}=0 \frac{\sqrt[2 n]{f(x)}}{g(x)}=0](https://lms.smart-osvita.org/filter/tex/pix.php/6d5949a586baba5a1d46d72c6d33d4d4.gif) рівносильне системі
рівносильне системі 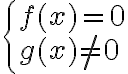
Теорема 7. Рівняння вигляду ![\frac{g(x)}{\sqrt[2 n]{f(x)}}=0 \frac{g(x)}{\sqrt[2 n]{f(x)}}=0](https://lms.smart-osvita.org/filter/tex/pix.php/1a4dbd2c424905744cec9bd0295c24a2.gif) рівносильне системі
рівносильне системі 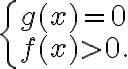
Звучить складно, проте насправді все не так страшно. Розпочнемо із ОДЗ.
Областю визначення рівняння, або областю його допустимих значень (ОДЗ), називається множина значень невідомого, при яких мають зміст його ліва і права частини.
В одних випадках знаходження ОДЗ є корисним для розв’язання рівнянь, в інших задача визначення ОДЗ є складною і непотрібною.
Радикали парного степеня є арифметичними, тобто ![\sqrt[2 n]{a} \geq 0 \sqrt[2 n]{a} \geq 0](https://lms.smart-osvita.org/filter/tex/pix.php/38020d56ecce094c0111f838330621e3.gif) , якщо
, якщо 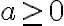 . Радикали непарного степеня визначені при будь-якому дійсному значенні підкореневого виразу. Виходячи з цих властивостей, у ряді випадків можна розв’язати ірраціональні рівняння без перетворень.
. Радикали непарного степеня визначені при будь-якому дійсному значенні підкореневого виразу. Виходячи з цих властивостей, у ряді випадків можна розв’язати ірраціональні рівняння без перетворень.
Приклад 1. Розв’язати рівняння 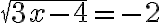 .
.
Ця рівність неправильна, бо 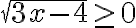 (за означенням арифметичного квадратного кореня). Отже, дане рівняння коренів не має.
(за означенням арифметичного квадратного кореня). Отже, дане рівняння коренів не має.
Приклад 2. Розв’язати рівняння 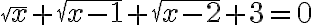 .
.
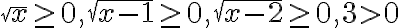 . Отже, значення лівої частини рівняння більше від
. Отже, значення лівої частини рівняння більше від 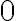 , точніше
, точніше 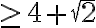 , і ніяк не може дорівнювати
, і ніяк не може дорівнювати 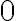 .
.
Приклад 3. Розв’язати рівняння 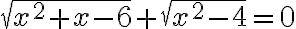 .
.
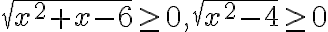 . Отже, дана рівність можлива тільки
. Отже, дана рівність можлива тільки
Приклад 4. Розв’язати рівняння ![\sqrt[4]{4-x}=3 x+\sqrt{x-5} \sqrt[4]{4-x}=3 x+\sqrt{x-5}](https://lms.smart-osvita.org/filter/tex/pix.php/26435f9bf48601a09e9ecf26551e3594.gif) .
.
Маємо: ОДЗ даного рівняння — це порожня множина, отже, розв’язувати рівняння немає потреби.
Приклад 5. Розв’язати рівняння 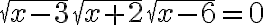 .
.
Маємо добуток, що дорівнює нулю. Отже,
Але при 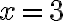 вираз
вираз 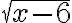 не має змісту, при
не має змісту, при 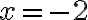 корені
корені 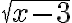 і
і 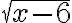 не існують, отже, числа
не існують, отже, числа 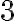 і
і  не є коренями даного рівняння.
не є коренями даного рівняння.
Приклад 6. Розв’язати рівняння ![\sqrt{x-3} \sqrt{x+2} \sqrt[3]{x-6}=0 \sqrt{x-3} \sqrt{x+2} \sqrt[3]{x-6}=0](https://lms.smart-osvita.org/filter/tex/pix.php/eed201f15973c7faf299780f7b662203.gif) .
.
Маємо добуток, що дорівнює нулю. Отже,
Але при 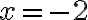 не існує
не існує 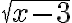 . Вираз
. Вираз ![\sqrt[3]{x-6} \sqrt[3]{x-6}](https://lms.smart-osvita.org/filter/tex/pix.php/9b147acb755fad18464c2cd353577a9e.gif) існує і при
існує і при 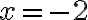 , і при
, і при 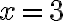 , бо підкореневий вираз кореня непарного степеня може набувати будь-яких дійсних значень.
, бо підкореневий вираз кореня непарного степеня може набувати будь-яких дійсних значень.
Джерело: Математика. Ірраціональні рівняння, нерівності та їх сис- М 34 теми : практикум / уклад. : Н.П. Муранова, Л.А. Харченко, Г.В. Шевченко, О.С. Муранов. – 2-е вид., стер. – К. : НАУ, 2012. – 96 с
Метод оцінювання: Краща оцінка.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour
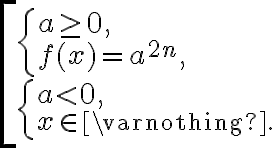
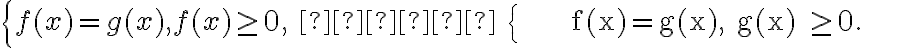
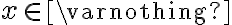
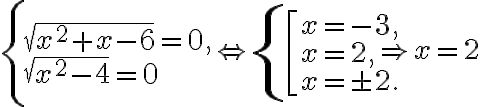
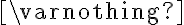
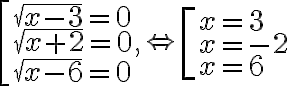
![\left[\begin{array} { l }
{ \sqrt { x - 3 } = 0 } \\
{ \sqrt { x + 2 } = 0 , } \\
{ \sqrt [3]{ x - 6 } = 0 }
\end{array} \Leftrightarrow \left[\begin{array}{l}
x=3 \\
x=-2 \\
x=6
\end{array}\right.\right. \left[\begin{array} { l }
{ \sqrt { x - 3 } = 0 } \\
{ \sqrt { x + 2 } = 0 , } \\
{ \sqrt [3]{ x - 6 } = 0 }
\end{array} \Leftrightarrow \left[\begin{array}{l}
x=3 \\
x=-2 \\
x=6
\end{array}\right.\right.](https://lms.smart-osvita.org/filter/tex/pix.php/6065ea666e62faef462a0f199e39c6b4.gif)