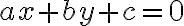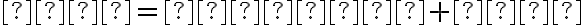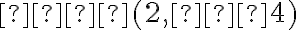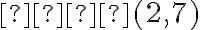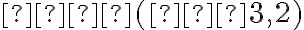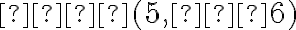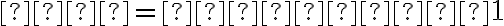Математика jul_2024_9_5: Рівняння прямої | Smartosvita LMS

Рівняння прямої

Загальне рівняння прямої на площині має вигляд

$ax+by+c=0$

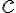де $a$ , $b$ і $c$ — деякі числа, причому a і b не дорівнюють нулю одночасно.

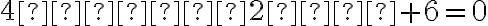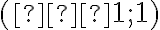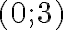Наприклад, рівняння $4𝑥−2𝑦+6=0$ задає пряму на площині. Щоб її побудувати, нам достатньо взяти дві точки, які належать даній прямій (перетворюють дану рівність у тотожність), позначити їх на координатній площині та провести пряму лінію через ці дві точки. Легко перевірити, що точки $(−1; 1)$ та $(0; 3)$ лежать на даній прямій. Позначивши ці точки на координатній площині та з’єднавши їх, ми отримуємо дану пряму.

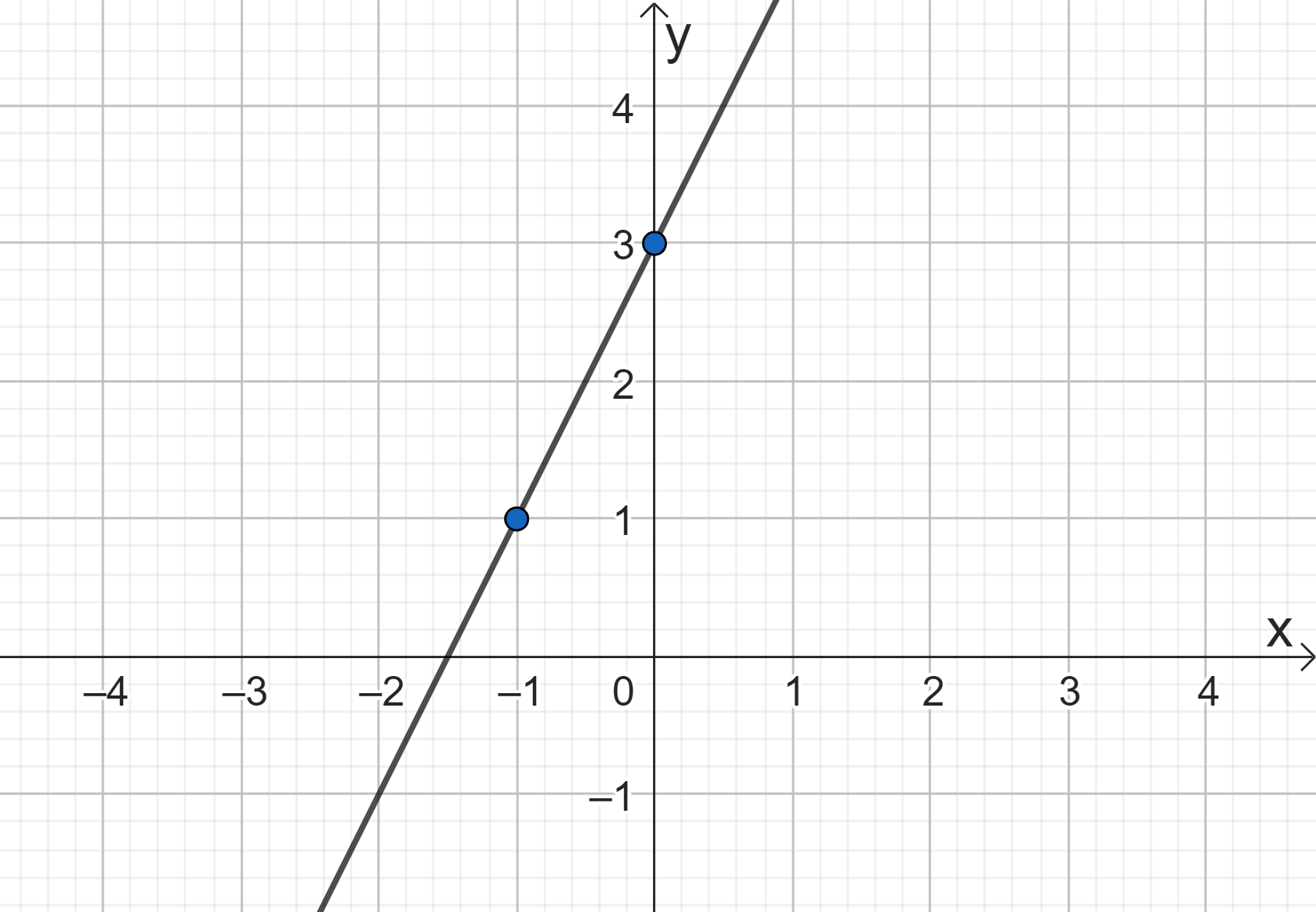
У випадку, коли 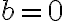$b = 0$ ми отримуємо рівняння 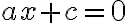$ax + c = 0$ . З цього рівняння можна легко виразити 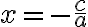$x=-\frac{c}{a}$ . Дана пряма проходить через точку 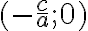$(-\frac{c}{a};0)$ перпендикулярно до осі 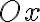$Ox$ (паралельно до осі $Oy$ ).

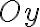У випадку, коли 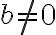$b\neq 0$ загальне рівняння прямої зручно переписати у вигляді

$𝑦=𝑘𝑥+𝑏$

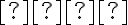де $𝑘$ є кутовим коефіцієнтом прямої, а 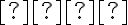$𝑏$ — вільним членом, який показує точку перетину прямої з віссю ординат.

У нашому випадку 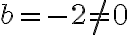$b =-2\neq 0$ , тому, виразивши 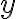$y$ , матимемо: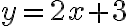 $y = 2x + 3$

Задача. Знайди рівняння прямої, яка проходить через точки:

1. $𝑃 (2,−4)$ і $𝑄 (2,7)$ ;

2. $𝑀 (−3, 2)$ і $𝑁 (5,−6)$ .

Розв’язання:

1. Оскільки дані точки мають однакові абсциси, пряма 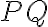$PQ$ є вертикальною, і її рівняння має вигляд $𝑥=2$ .

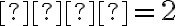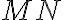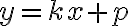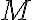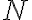2. Оскільки дані точки мають різні абсциси, то пряма $MN$ не є вертикальною, тому скористаємося рівнянням прямої у вигляді $y = kx + p$ . Підставивши координати точок $M$ і $N$ у дане рівняння, отримуємо систему рівнянь:

\begin{cases} -3k+p=2,\\ 5k+p=-6 \end{cases}

Розв’язавши цю систему рівнянь, знаходимо, що 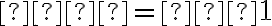$𝑘=−1$ , $𝑝=−1$ .

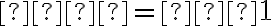Відповідь:

1. $𝑥=2$ ;

2. $𝑦=−𝑥−1$ .

_{Теорію розробила Грибель Ольга.}
_{Картинку до теорії створила Грибель Ольга в Geogebra.}

Метод оцінювання: Краща оцінка.