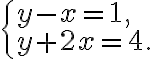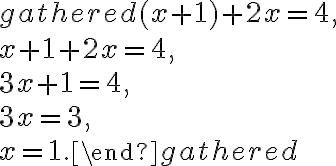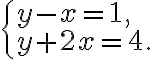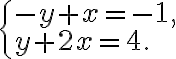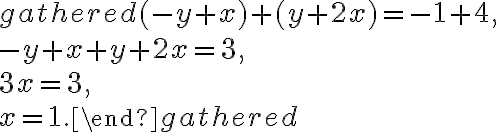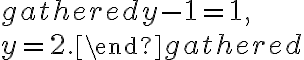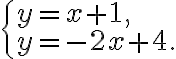Системи рівнянь із двома змінними
Система рівнянь — це набір двох або більше рівнянь, які мають спільні змінні та розглядаються одночасно. Основна мета розв’язування систем рівнянь полягає у знаходженні значень змінних, які задовольняють кожне з рівнянь системи (перетворюють кожне з рівнянь системи у тотожну рівність).
Загалом кількість рівнянь і змінних у системі може бути будь-якою, але ми зосередимо увагу на розв’язуванні систем з двох рівнянь із двома змінними. Є декілька методів розв’язування таких систем, але ми розглянемо тільки три найпоширеніші: метод підстановки, метод додавання і графічний метод.
Метод підстановки полягає у тому, що з одного з рівнянь системи виражається одна змінна через іншу, а потім підставляється у друге рівняння.
Алгоритм:
- Вибери одне з рівнянь системи і вирази у ньому одну змінну через іншу.
- Підстав отримане вираження у друге рівняння системи.
- Розв’яжи отримане рівняння однієї змінної.
- Знайдене значення змінної підстав у вираз, отриманий на першому кроці, щоб знайти значення другої змінної.
- Запиши відповідь.
Приклад:
Розглянемо систему рівнянь:
Розв’яжемо дану систему рівнянь методом підстановки. Спочатку виразимо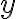 
через 
із першого рівняння: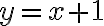 
. Підставимо отриманий вираз у друге рівняння системи:
Тепер знайдемо y, підставивши отримане значення у вираз для :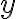 
.
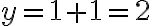Отже, розв’язком нашої системи рівнянь є пара чисел: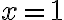 
, 
.
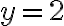Метод додавання полягає у тому, що одне з рівнянь множиться на таке число, щоб коефіцієнти перед однією зі змінних стали протилежними, а потім обидва рівняння додаються, в результаті чого одна зі змінних зникає.
Алгоритм:
- Помнож одне або обидва рівняння на такі числа, щоб коефіцієнти перед однією зі змінних стали протилежними.
- Додай обидва рівняння (на цьому етапі одна зі змінних має зникнути).
- Розв’яжи отримане рівняння однієї змінної.
- Знайдене значення змінної підстав в одне з початкових рівнянь системи і знайди другу змінну.
- Запиши відповідь.
Приклад:
Давай знову розглянемо попередню систему рівнянь, але цього разу розв’яжемо її методом додавання:
Помножимо перше рівняння нашої системи на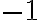 
, щоб зробити коефіцієнт біля змінної 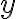в першому рівнянні протилежним до коефіцієнта біля змінної 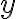в другому рівнянні. Після виконання множення отримаємо наступну систему:
Тепер наша система готова до додавання. Додамо обидва рівняння (ліву частину до лівої, а праву до правої):
Тепер знайдемо 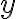, підставивши отримане значення в одне з рівнянь системи (давай підставимо у перше рівняння):
Отже, як і в попередньому випадку, ми отримали, що 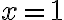, 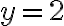є розв’язком нашої системи рівнянь.
Виходить, що метод розв’язання не змінює кількість розв’язків.
Графічний метод полягає в побудові графіків рівнянь на одній координатній площині та знаходженні точок перетину. Точки перетину графіків і є розв’язком системи.
Алгоритм:
- Розв’яжи кожне рівняння відносно 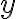(якщо це необхідно).
- Побудуй графіки обох рівнянь на одній координатній площині.
- Знайди точки перетину графіків, які й будуть розв’язком системи.
- Запиши відповідь.
Приклад:
Розв’яжемо нашу систему рівнянь графічним методом. Спершу запишемо кожне з рівнянь системи у формі, зручній для побудови графіків:
Зауважимо, що ці рівняння задають прямі на площині. Побудуємо ці прямі на одній координатній площині, щоб візуально побачити розв’язки системи рівнянь (розв’язки будуть розташовуватися на перетині графіків).
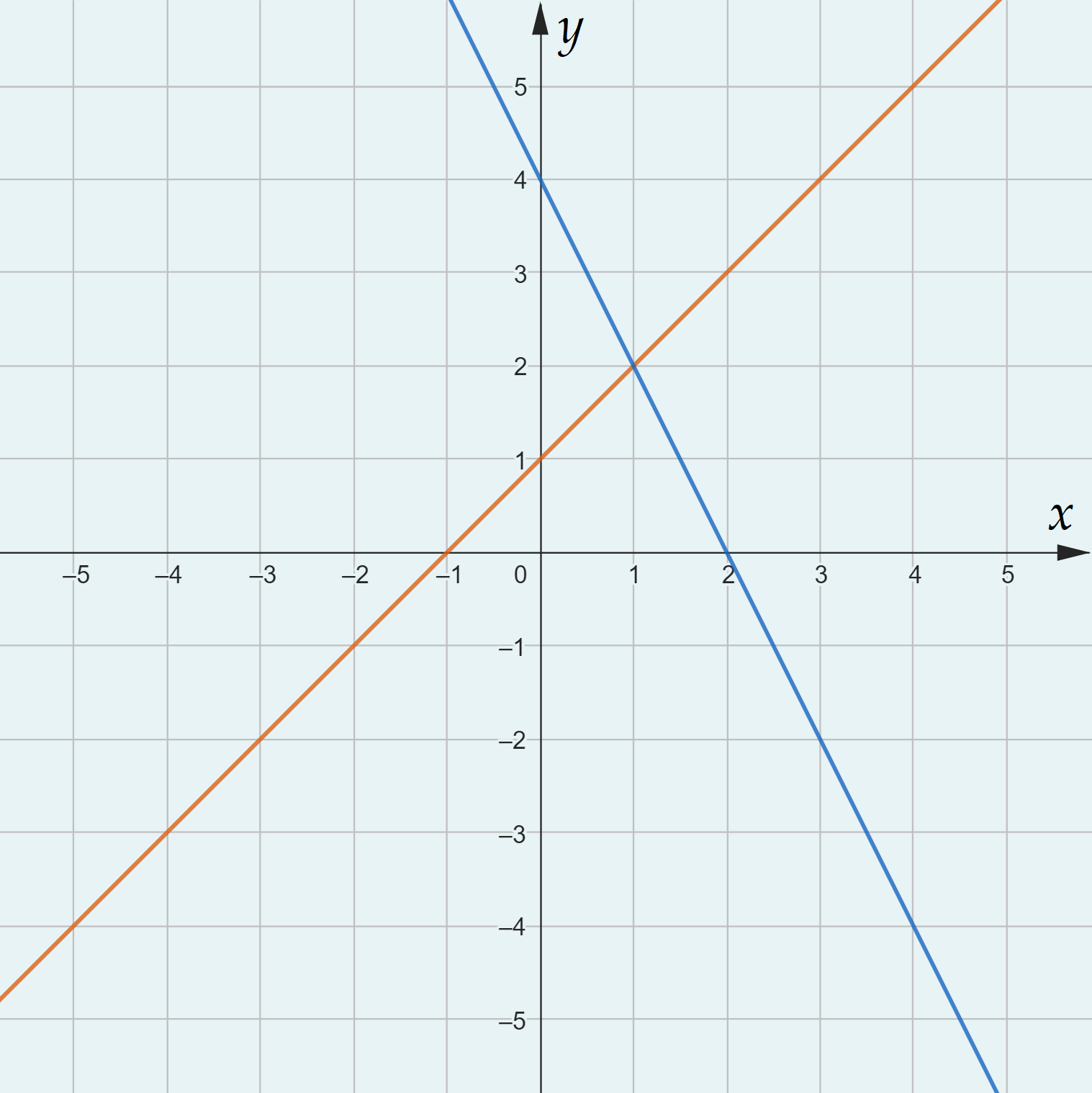
Бачимо, що графіки перетинаються в точці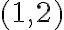 
, що означає, що 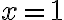, 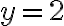є розв’язком системи рівнянь.
Ми розглянули три основні методи розв’язання систем рівнянь: метод підстановки, метод додавання і графічний метод. Кожен з них має свої переваги і може бути раціональнішим у деяких конкретних випадках. Зауважимо, що для розв’язування систем двох рівнянь другого степеня з двома змінними іноді зручно використовувати метод заміни змінних, який допомагає значно спростити систему. Навчися застосовувати кожен із методів, і ти зможеш вибирати кращий метод для конкретної системи.
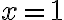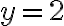, є розв’язком нашої системи рівнянь. 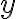(якщо це необхідно).Бачимо, що графіки перетинаються в точці 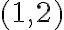, що означає, що 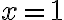, 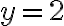є розв’язком системи рівнянь.
Ми розглянули три основні методи розв’язання систем рівнянь: метод підстановки, метод додавання і графічний метод. Кожен з них має свої переваги і може бути раціональнішим у деяких конкретних випадках. Зауважимо, що для розв’язування систем двох рівнянь другого степеня з двома змінними іноді зручно використовувати метод заміни змінних, який допомагає значно спростити систему. Навчися застосовувати кожен із методів, і ти зможеш вибирати кращий метод для конкретної системи.
Текст розробила Грибель Ольга з використанням ChatGPT-4.0.
Картинку до тексту створила Грибель Ольга в GeoGebra+Paint.
Метод оцінювання: Краща оцінка.