Математика jul_2024_8_8: Коренева функція | Smartosvita LMS

Коренева функція

Тепер заглянемо у корінь ;)

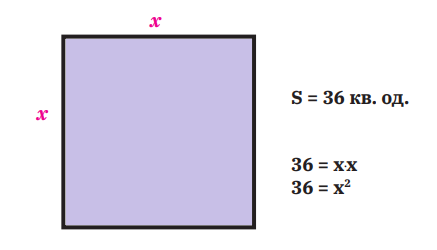
Розглянемо квадрат, площа якого дорівнює 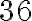$36$ квадратних одиниць. Нехай довжина його сторони дорівнює 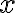$x$ одиниць. Тоді рівняння 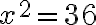$x^2=36$ можна розглядати як математичну модель задачі про знаходження сторони квадрата, площа якого дорівнює 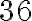$36$ квадратних одиниць.

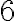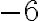Коренями цього рівняння є числа $6$ і $-6$ . Ці числа є квадратними коренями з числа $36$ .

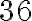Отже, квадратним коренем із числа 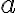$a$ називають число, квадрат якого дорівнює числу $a$ .

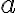Щодо нашого квадрата, то, звісно, лише додатний корінь рівняння 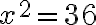$x^2=36$ , тобто число 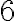$6$ , є відповіддю до задачі про знаходження сторони квадрата, площа якого дорівнює 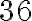$36$ квадратним одиницям. Це число називають арифметичним квадратним коренем із числа $36$ .

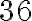Тож арифметичним квадратним коренем із числа 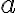$a$ називають невід’ємне число, квадрат якого дорівнює $a$ .

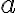Арифметичний квадратний корінь із числа 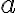$a$ позначають 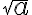$\sqrt{a}$ . Знак називають знаком квадратного кореня або радикалом.

Площу квадрата знаходять за формулою 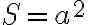$S=a^2$ .

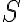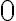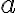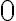Оскільки $S$ > $0$ і $a$ > $0$ , то з формули площі квадрата можемо виразити його сторону: 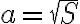$a=\sqrt{S}$ . Ця формула задає функціональну залежність, для якої незалежною змінною тепер є площа квадрата 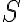$S$ , а залежною змінною — довжина сторони квадрата 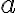$a$ . Справді, зі зміною площі квадрата відповідно змінюється й довжина його сторони. Якщо незалежну змінну позначити як 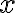$x$ , а залежну — як 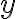$y$ , то одержимо функцію $y=\sqrt{x}$ .

Основні властивості функції $y=\sqrt{x}$ :

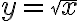Область визначення — всі невід’ємні числа. Область значень — всі невід’ємні числа. Графік — вітка параболи. Точка 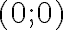$(0;0)$ — точка перетину графіка з осями координат. Функція є зростаючою на всій області визначення.

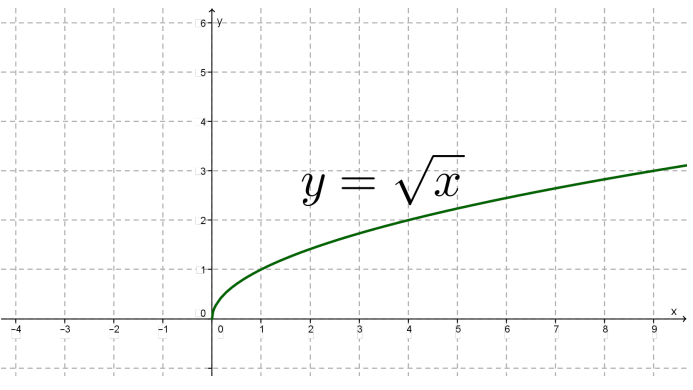
Теорію впорядкувала Расяк Юлія з використанням ChatGPT-3.5.

Рисунки до теорії взято з мережі.

Метод оцінювання: Краща оцінка.