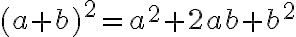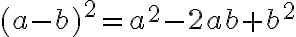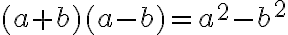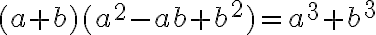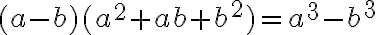Математика jul_2024_7_9: Виконує кожен. Розпізнаємо формули скороченого множення | Smartosvita LMS

Виконує кожен. Розпізнаємо формули скороченого множення

Квадрат суми

Пригадай, що двочленом ми називаємо многочлен, що складається з двох доданків.

Що буде, якщо піднести двочлен до квадрата?

Ні-ні, не роби так, як на цій картинці 🙂.

Отож, піднести до квадрата — це помножити на себе ж. Піднесемо до квадрата вираз 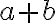$a+b$ :

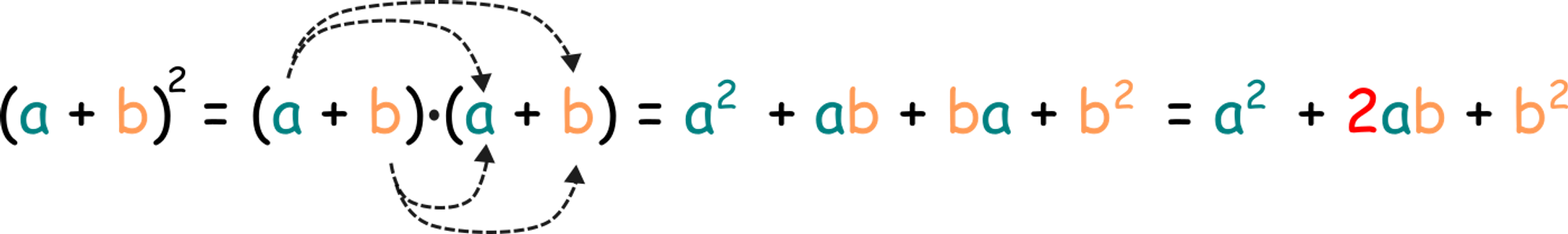
Ми отримали формулу скороченого множення, яку ще називають формулою квадрата суми:

$(a+b)^2=a^2+2ab+b^2$ .

Розглянь цікаве геометричне доведення. Сторона квадрата дорівнює 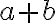$a+b$ , а тому 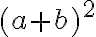$(a+b)^2$ — площа квадрата. А з іншого боку, цей квадрат складається з двох блакитних прямокутників та зеленого й рожевого квадратів. Додавши їхні площі, отримаємо нашу формулу.

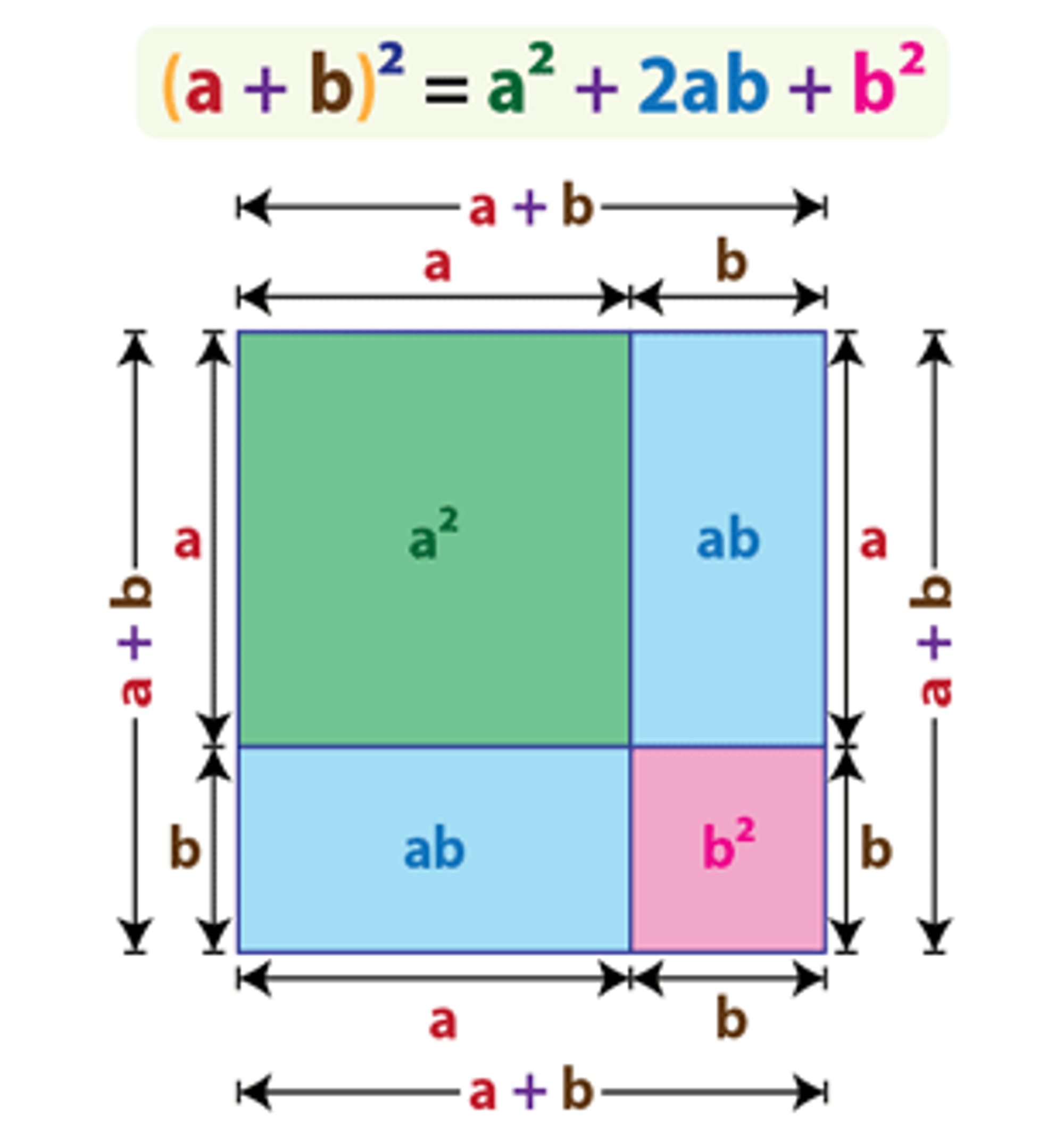
Квадрат різниці

А що буде, якщо піднести до квадрата двочлен $a-b$ ?

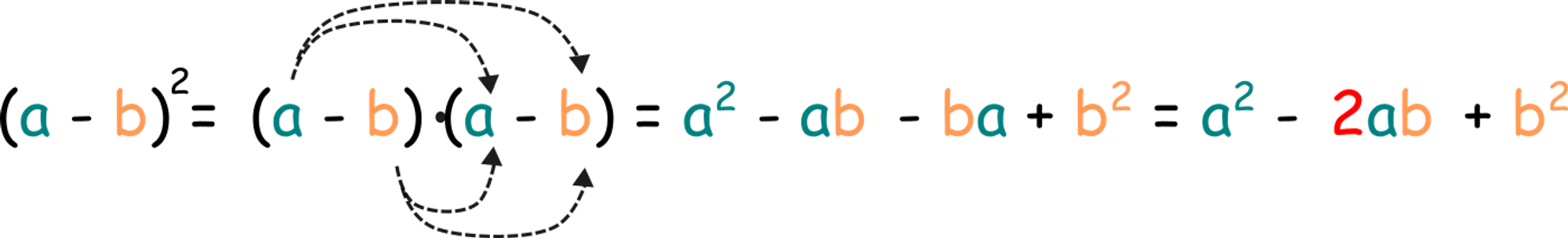
Отримали формулу квадрата різниці:

$(a-b)^2=a^2-2ab+b^2$ .

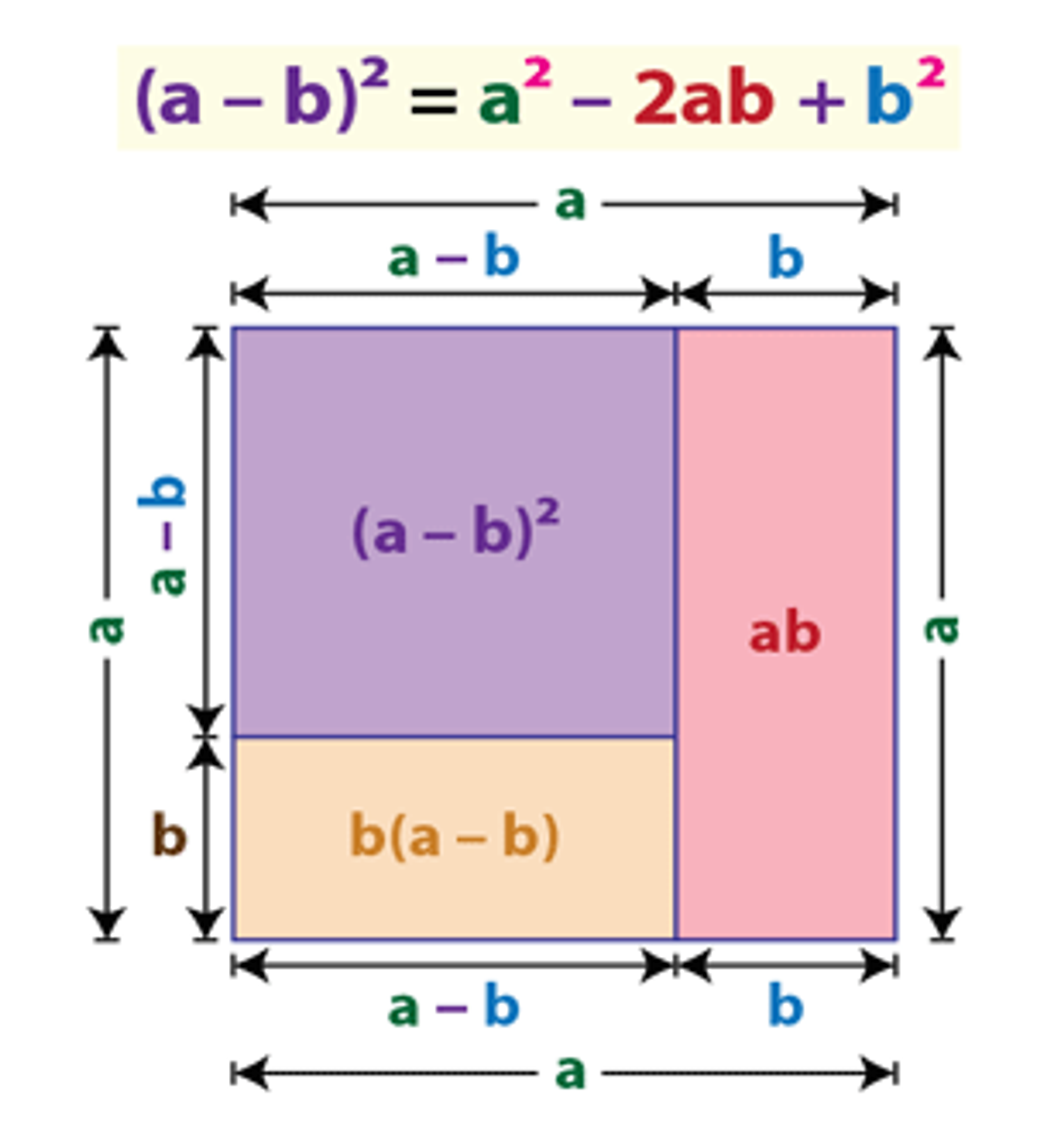
Ось геометричне доведення. Спробуй розібратися в ньому самостійно.

Добуток суми виразів на їх різницю

Тепер перемножимо двочлени 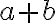$a+b$ і $a-b$ :

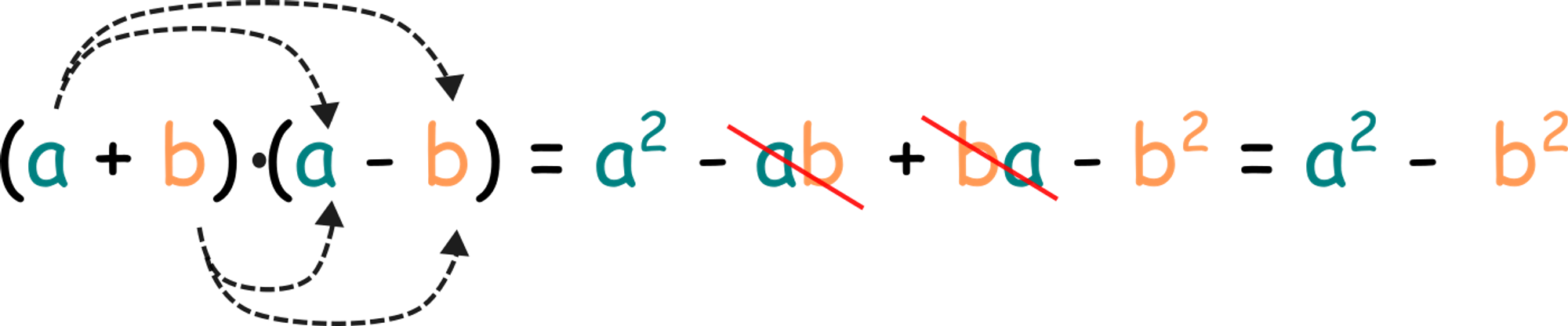
Отримали формулу скороченого множення:

$(a+b)(a-b)=a^2-b^2$ .

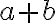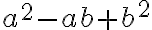Виведемо ще одну формулу для швидкого множення. Розглянемо вирази $a+b$ та $a^2-ab+b^2$ . Чи нагадує тобі щось другий множник? Так, він дуже схожий до квадрата різниці, лише не вистачає двійки перед $ab$ . Тому цей множник називають неповним квадратом різниці. Помножимо їх:

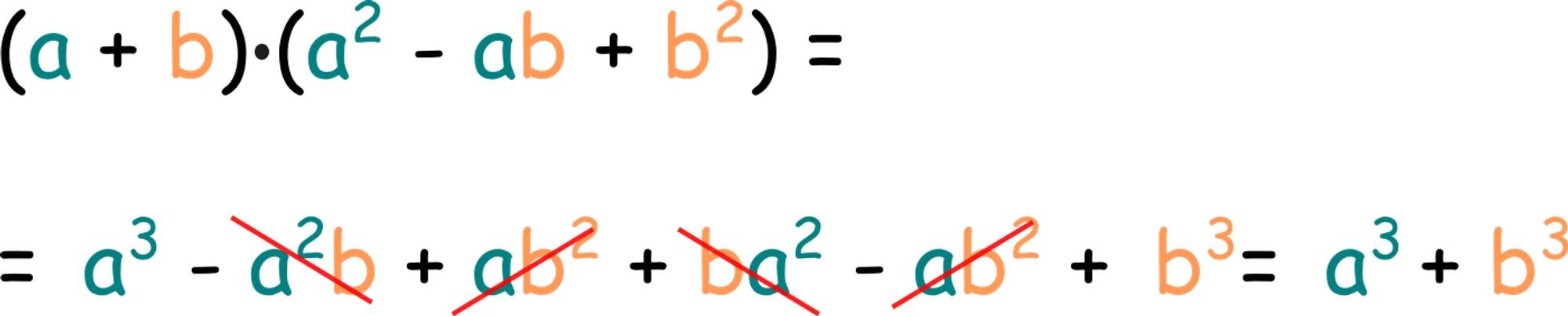
Маємо:

$(a+b)(a^2-ab+b^2)=a^3+b^3$ .

Тепер змінимо знаки в двочлені та перед $ab$ в тричлені:

Маємо таку формулу:

$(a-b)(a^2+ab+b^2)=a^3-b^3$ .

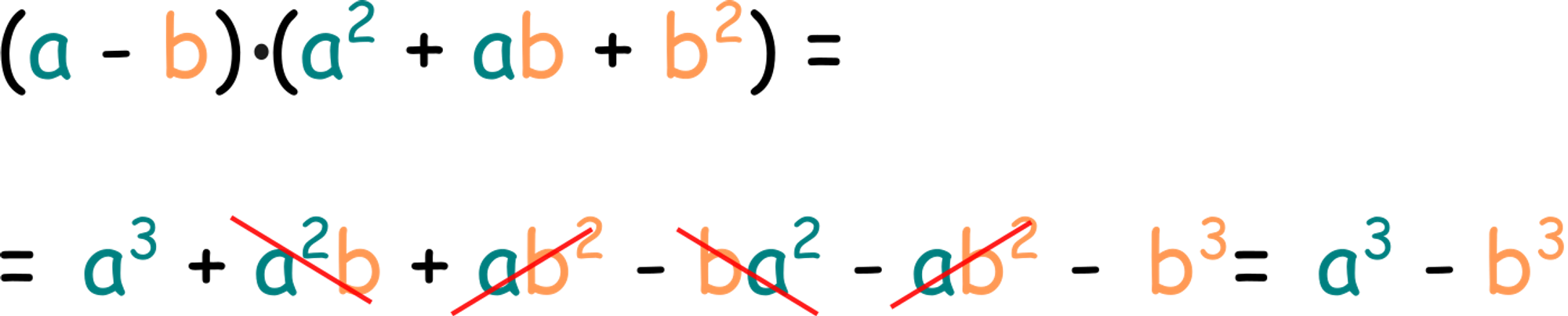
Отже, ми отримали 5 формул, які допоможуть тобі значно швидше справлятися з множенням виразів на практиці:

$(a+b)^2=a^2+2ab+b^2$ ;

$(a-b)^2=a^2-2ab+b^2$ ;

$(a+b)(a-b)=a^2-b^2$ ;

$(a+b)(a^2-ab+b^2)=a^3+b^3$ ;

$(a-b)(a^2+ab+b^2)=a^3-b^3$ .

_{Текст розробила Козінчук Віра.}
_{Ілюстації до геометричного доведення}
_{взято з mathworksheets4kids.com.}

_{Картинки-формули створила}
_{Козінчук Віра в Inkscape.}

Метод оцінювання: Краща оцінка.

Accessibility

Background Colour

Font Face

Font Kerning

Font Size

1

Image Visibility

Letter Spacing

0

Line Height

1.2

Link Highlight

Text Colour